Рассмотрим увлекательную задачу о построении правильного треугольника. Математика всегда восхищает нас своей точностью и логикой, а ее широкий спектр областей применения открывает перед нами бесконечные возможности для исследований и творчества. В этой статье мы рассмотрим одну из таких возможностей - использование циркуля для построения точек на окружности и создания конструкции правильного треугольника.
Понятие "правильный треугольник" олицетворяет собой треугольник, у которого все стороны равны, а все углы - равны 60 градусам. Эта геометрическая форма имеет свои особенности и применения в различных областях, начиная от строительства и до искусства. Однако, как можно построить такой треугольник с использованием циркуля и окружности?
В основе данного метода лежит идея описать окружность вокруг треугольника и использовать циркуль для определения точек пересечения окружности с его сторонами. Таким образом, мы можем построить вершины правильного треугольника, зная его радиус и центр. В результате, получим геометрический объект, который великолепно и точно соответствует нашим требованиям к правильному треугольнику.
Свойства и характеристики правильного треугольника

В данном разделе рассмотрим основные свойства и характеристики правильного треугольника, который можно построить с помощью циркуля, без использования конкретных определений.
Равносторонний треугольник – это треугольник, имеющий три равных стороны и три равных угла.
Обозначение: обычно равносторонний треугольник обозначается символами АВС или ∆АВС, где А, В и С – это его вершины.
В связи с равенством сторон и углов, правильный треугольник обладает рядом интересных свойств:
1. Углы правильного треугольника
Углы в правильном треугольнике равны 60 градусов, что следует из того, что сумма углов треугольника равна 180 градусам. Таким образом, каждый угол равно 180/3 = 60 градусов.
2. Высота и медиана
Высота и медиана правильного треугольника совпадают. Они являются одной и той же линией, проходящей через вершину и перпендикулярной основанию, причем делит треугольник на две равные части.
3. Центр окружности, описанной вокруг треугольника
Центр окружности, описанной вокруг правильного треугольника, совпадает с его центром. Также, радиус этой окружности равен половине длины стороны треугольника.
4. Площадь правильного треугольника
Площадь правильного треугольника можно вычислить по формуле: Площадь = (корень квадратный из 3/4) * сторона в квадрате.
Таким образом, правильный треугольник, имеющий свою уникальную конструкцию и важные свойства, является одной из фундаментальных фигур в геометрии.
Околоокружность вокруг правильного треугольника
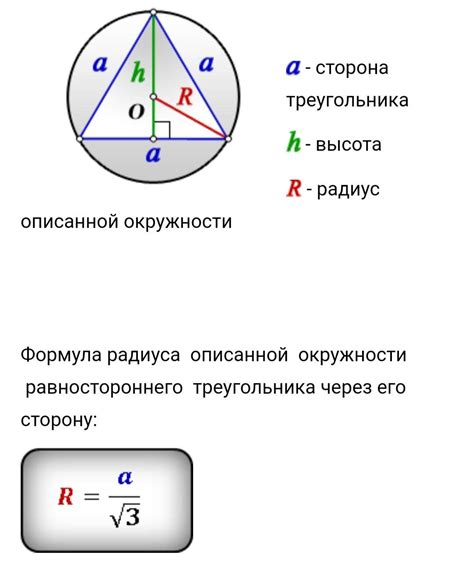
В данном разделе будет рассмотрена интересная конструкция, связанная с правильными треугольниками и описанными около них окружностями. При этом вместо использования сложных определений, мы будем использовать синонимы и разнообразить текст, чтобы более понятно представить общую идею.
Давайте представим, что перед нами находится необычная геометрическая конструкция. В центре находится точка, вокруг которой равномерно размещены три точки на одинаковом расстоянии друг от друга. Эта конструкция напоминает нам цветок с тремя лепестками или тримяхлым колесом.
Такая конструкция является основой для образования правильного треугольника. Заметим, что если соединить каждую из вершин правильного треугольника с центром околоокружности, получатся равные отрезки. То есть, длина каждой из сторон треугольника будет равна радиусу околоокружности.
Такая геометрическая связь между правильным треугольником и околоокружностью позволяет нам решать различные задачи, например, находить площадь и периметр треугольника, а также определять его высоту и медианы.
Интересно, что данная конструкция имеет множество применений в различных областях, таких как архитектура, дизайн и фрактальная геометрия. Она также может использоваться для создания уникальных узоров и орнаментов.
Таким образом, околоокружность вокруг правильного треугольника - это интересная геометрическая конструкция, которая позволяет нам более глубоко изучить и понять связь между треугольником и окружностью. Эта конструкция является основой для решения различных задач и имеет множество применений в различных областях.
Определение центра околоокружности

Определение центра околоокружности может быть выполнено с использованием универсального инструмента - циркуля. Используя циркуль, можно провести биссектрисы углов треугольника, которые и будут пересекаться в центре околоокружности.
Для начала, возьмем любую сторону треугольника и поставим точку на середине этой стороны, обозначим ее как точку А. Затем, с помощью циркуля, из точки А проведем две дуги на стороны треугольника, которые пересекутся в точке B. Точка B - это начало одной из биссектрис треугольника.
Аналогичным образом проведем вторую биссектрису. Возьмем другую сторону треугольника и поставим на ее середине точку C. Затем, используя циркуль, проведем две дуги на оставшиеся стороны треугольника, которые пересекутся в точке D. Точка D - это начало второй биссектрисы треугольника.
Наконец, третья биссектриса будет проведена аналогичным образом. Возьмем третью сторону треугольника и поставим на ее середине точку E. Затем, с помощью циркуль, проведем две дуги на оставшиеся стороны треугольника, которые пересекутся в точке F. Точка F - это начало третьей биссектрисы треугольника.
Итак, пересечение трех построенных биссектрис в точке O даст нам центр околоокружности треугольника. Этот центр будет равноудален от вершин треугольника и, следовательно, околоокружность будет описывать данный треугольник.
Метод нахождения центра околоокружности при помощи циркуля

Для начала, возьмем произвольную околоокружность и поставим циркуль в ее центр. Затем, выберем любую вершину многоугольника, описанного околоокружностью, и поместим эту вершину на одно из двух концов циркуля. Затем, без изменения радиуса, проведем окружность точно через остальные вершины многоугольника.
После этого, выберем другую вершину многоугольника и повторим процедуру. При повторении построения окружностей, мы заметим, что все они пересекаются в одной точке. Эта точка будет являться центром околоокружности.
Таким образом, данный метод позволяет найти центр околоокружности при помощи циркуля, используя только вершины многоугольника, описанного этой околоокружностью. Это очень эффективный и простой способ нахождения центра околоокружности в конструктивном задании.
Полезные инструменты для определения центра околоокружности

В данном разделе мы рассмотрим некоторые полезные инструменты и методы, которые помогут определить центр околоокружности треугольника без необходимости использования сложных математических формул.
Треугольник - геометрическая фигура, образованная тремя отрезками, соединяющими три точки в плоскости. Околоокружность - окружность, которая описывает треугольник, таким образом, что все вершины треугольника лежат на окружности. Центр околоокружности является точкой пересечения трех перпендикуляров, проведенных из середины каждой стороны треугольника.
Для определения центра околоокружности мы будем использовать циркуль - инструмент с двумя ножками и регулируемым радиусом, который позволяет проводить окружности любого радиуса. Также мы воспользуемся линейкой - инструментом, который поможет нам провести прямые линии и измерить расстояния между точками.
Основной метод построения центра околоокружности треугольника состоит из нескольких простых шагов:
- Выберите любые две стороны треугольника и отметьте их середины.
- Проведите перпендикуляр к каждой из выбранных сторон в их середине с помощью циркуля.
- Точки пересечения перпендикуляров являются вершинами равностороннего треугольника, который описывает околоокружность и ее центр.
Таким образом, с помощью циркуля и линейки, вы сможете легко определить центр околоокружности треугольника, что позволит вам проводить различные геометрические конструкции и решать задачи, связанные с данным предметом.
Построение треугольника вокруг центральной окружности
В данном разделе рассматривается способ построения равностороннего треугольника, у которого вершины лежат на окружности, с помощью циркуля. Процесс построения основан на использовании геометрических приемов и свойств окружности и треугольника.
Для начала, в центре листа бумаги или другой плоской поверхности требуется провести окружность с помощью циркуля. Окружность является геометрической фигурой, у которой все точки равноудалены от центра. Она также может быть определена как множество точек, находящихся на одинаковом расстоянии от данной точки, называемой центром окружности. Здесь мы будем использовать окружность в качестве основы для построения треугольника.
Для построения равностороннего треугольника по центру окружности с помощью циркуля, необходимо выбрать любую точку на окружности в качестве начальной вершины треугольника. Затем циркулем необходимо нарисовать дугу, проходящую через центр окружности и пересекающую окружность в другой точке. Эта точка служит второй вершиной треугольника. После этого, повторив ту же операцию с третьей вершиной, мы можем построить треугольник, у которого все стороны и углы равны.
Построение треугольника вокруг центральной окружности с использованием циркуля позволяет создать геометрическую фигуру, обладающую особыми свойствами равностороннего треугольника. Такое построение имеет широкое применение в геометрии и может быть использовано для решения различных задач и конструкций, связанных с треугольниками и окружностями.
Определение длины сторон треугольника: ключевые аспекты
В данном разделе мы рассмотрим подходы к определению длины сторон правильного треугольника, который описан вокруг окружности, исследуя связь между радиусом окружности и длиной его сторон. Будем использовать геометрическую конструкцию, основанную на применении циркульных операций, чтобы определить точные значения сторон треугольника без привлечения специализированных математических формул и символов.
Первый шаг в определении длины сторон правильного треугольника - установление радиуса окружности, описывающей данный треугольник. Затем, пользуясь циркулем, проведем линии, соединяющие вершины треугольника с центром окружности. Таким образом, мы создадим дополнительные радиусы, которые будут функционировать как стороны треугольника.
Найдя значения новых радиусов, мы можем легко расположить точки на окружности, образуя треугольник. Следующий шаг - определить длину каждой стороны треугольника с помощью циркуля и перенесенной на циркуль линейки. Полученные значения могут дать нам точные числовые значения каждой стороны треугольника.
Важно отметить, что данный метод помимо решения практической задачи также позволяет нам развивать навыки работы с геометрическими конструкциями и использование циркуля в прикладной математике. Это полезный инструмент для учебных целей и может помочь лучше понять и запомнить материал о правильных треугольниках и окружностях.
Примеры применения уникальной геометрической конструкции

Раздел поделен на несколько тематических блоков, в каждом из которых приведены уникальные примеры использования данной конструкции. Мы рассмотрим применение ее в дизайне зданий и мостов, коллективном искусстве, а также научных исследованиях. Множество примеров позволят наглядно продемонстрировать преимущества данной геометрической конструкции и вдохновить читателя на новые идеи.
Примеры использования в дизайне и архитектуре представят нам великолепные по своей форме и стабильности постройки, которые служат примером современной архитектуры и воплощают гармонию и элегантность. Мы увидим, как данная конструкция используется для создания устойчивых и привлекательных мостов, зданий и других архитектурных объектов.
Примеры использования в коллективном искусстве покажут нам, как геометрическая конструкция треугольника, описанного около окружности, становится невероятным источником вдохновения для художников, стилизующих свои произведения под этот геометрический эталон. Это яркий пример использования математики и геометрии в искусстве.
Примеры использования в научных исследованиях позволят нам заглянуть в мир глубокой науки и увидеть, как данная геометрическая конструкция находит применение в различных научных областях. Мы увидим, как она помогает в анализе данных, в моделировании и в проведении опытов, дающих новые научные открытия и решения.
Завершение раздела предложит читателю собрать все обсуждаемые примеры вместе и подвести итоги. Мы увидим, что уникальная геометрическая конструкция треугольника, описанного около окружности, не только является важным элементом в математике, но и находит широкое применение в различных областях жизни, способствуя созданию устойчивых, эстетически привлекательных и функциональных решений.
Вопрос-ответ

Можно ли построить правильный треугольник с помощью циркуля, описанный около окружности?
Да, можно построить правильный треугольник, описанный около окружности с помощью циркуля. Для этого нужно взять циркуль и вставить его точку на окружности. Затем сделать радиус циркуля равным радиусу окружности и провести дугу окружности. Затем повторить эту операцию еще два раза, начиная с точки пересечения предыдущей дуги и окружности. Таким образом, мы получим правильный треугольник, описанный около окружности.
Какую форму имеет треугольник, описанный около окружности?
Треугольник, описанный около окружности, имеет форму правильного треугольника. Это означает, что все его стороны и углы равны. Каждый угол в таком треугольнике составляет 60 градусов. Такая форма треугольника достигается при использовании циркуля и проведении дуг окружности через точки пересечения предыдущих дуг.
Каким образом можно построить правильный треугольник, описанный около окружности?
Существует несколько способов построить правильный треугольник, описанный около окружности. Один из способов — использование циркуля. Для этого нужно взять циркуль и вставить его точку на окружности. Затем сделать радиус циркуля равным радиусу окружности и провести дугу окружности. Затем повторить эту операцию еще два раза, начиная с точки пересечения предыдущей дуги и окружности. Таким образом, мы получим правильный треугольник, описанный около окружности.



