Многие люди, интересующиеся геометрией и математикой, задаются вопросом о том, как определить высоту призмы. И действительно, знание этого параметра позволяет нам лучше понять геометрическую форму призмы и решать различные задачи, связанные с ее свойствами. Высота призмы - это важная характеристика, которая помогает нам определить объем, площадь поверхности и другие параметры призмы.
Таким образом, выяснение высоты призмы является необходимым для осуществления дальнейших математических расчетов и построения конкретных моделей на основе призматических фигур. Определить высоту призмы можно с помощью геометрической формулы, основываясь на известных параметрах периметра основания, площади основания и объеме призмы. Однако для полного понимания данной темы необходимо разобраться в основных понятиях геометрии и знать элементарные операции с числами.
Чтобы решить проблему определения высоты призмы, нам следует ознакомиться с основными формулами и правилами, определяющими геометрические фигуры. Например, понимание того, что призма - это многогранник, состоящий из двух параллельных многоугольных оснований и всех перпендикулярных их граней, поможет нам лучше визуализировать данную фигуру и анализировать ее свойства. Кроме того, важно знать, что высотой призмы является расстояние между ее двумя параллельными основаниями, которое проходит через их центры.
Значимость формулы для вычисления высоты геометрической призмы
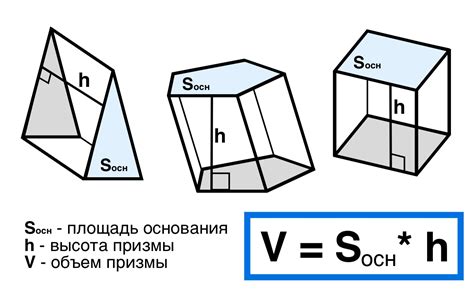
В данном разделе рассмотрим важность применения формулы, применяемой для определения высоты призмы в геометрии. Математическая формула позволяет нам расчетно определить указанную высоту с использованием других известных параметров.
Существует множество различных геометрических призм, и каждая из них имеет свою конкретную формулу для вычисления высоты. Это является основой для многих задач и расчетов в различных областях, таких как строительство, архитектура, видеоигры и другие.
Знание и применение формулы позволяет нам не только точно рассчитывать высоту призмы, но и получать полезную информацию о ее размерах и свойствах. Использование формулы также является неотъемлемой частью при решении различных геометрических задач, связанных с призмами.
Без использования формулы для определения высоты призмы, мы бы не смогли эффективно моделировать и анализировать различные объекты и конструкции в трехмерном пространстве. Формула позволяет нам получить точные значения и прогнозы, что способствует более точному проектированию и строительству.
Таким образом, понимание и применение формулы для определения высоты призмы имеет огромное значение в геометрии и приводит к более точным и успешным результатам в различных областях человеческой деятельности.
Суть математического выражения и его значение в расчете высоты призмы

Важно отметить, что данная формула представляет собой специфическую комбинацию чисел и символов, которая описывает связь между различными параметрами призмы, такими как ее площадь основания, объем или другие измерения. Разумное применение этой формулы позволяет определить по одному известному параметру высоту призмы.
- Формула призвана помочь в решении задач, связанных с высотой призмы;
- Важно понимать, что это только одно из возможных математических выражений, но часто используется по своей универсальности и эффективности в расчетах;
- Также необходимо помнить, что контекст и условия задачи могут требовать использования разных формул или методов, поэтому важно выбирать подходящее выражение на основе предоставленной информации;
- Понимание значения и принципов работы данной формулы позволяет производить точные и достоверные вычисления, что незаменимо при решении различных практических задач.
Использование известных параметров для вычисления высоты призмы
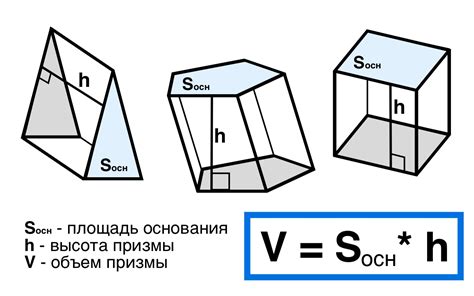
В данном разделе мы рассмотрим методы определения высоты призмы на основе имеющихся данных о ее параметрах. В случае, когда точное измерение высоты невозможно или затруднительно, можно использовать доступные характеристики для расчета данного значения.
Для вычисления высоты призмы можно использовать различные подходы, в зависимости от имеющихся данных. Один из таких подходов - использование формулы для расчета высоты призмы на основе известных аналогичных параметров, таких как площадь основания и объем призмы.
Для применения данного метода необходимо иметь знания о формулах и связи между параметрами призмы. Расчет высоты призмы на основе известных параметров позволяет получить более точное представление о геометрических характеристиках данного объекта.
Кроме того, для определения высоты призмы можно использовать соотношения между углами треугольника, образованного перпендикулярной прямой и боковыми гранями призмы. С использованием подобных методов вычисления можно получить сравнительно точные значения высоты призмы с ограниченными возможностями измерений.
Использование известных параметров для определения высоты призмы является важным инструментом в изучении геометрии и позволяет получить дополнительную информацию о данном геометрическом объекте. Грамотное применение соответствующих методов позволит получить более точные данные о высоте призмы, что является важным элементом при проведении различных расчетов и измерений.
Взаимосвязь параметров при расчете высоты призмы по формуле
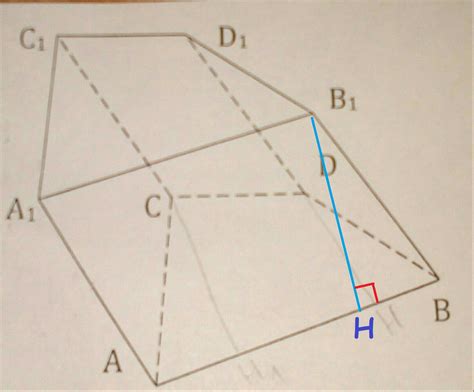
Один из основных параметров, необходимых для расчета высоты призмы, - это ее площадь основания. Площадь основания является важным показателем, поскольку она определяет количество пространства, занимаемого призмой в плоскости основания. Чем больше площадь основания, тем выше может быть высота призмы. Однако, стоит отметить, что площадь основания не является единственным фактором, влияющим на высоту призмы.
Другим параметром, который следует учитывать, является объем призмы. Объем призмы выражает величину пространства, занимаемого ею. Взаимосвязь между объемом и высотой призмы может быть представлена в виде формулы, в которой объем является результатом произведения площади основания на высоту. Таким образом, высота призмы будет зависеть от его объема и площади основания.
| Параметр | Описание | Взаимосвязь с высотой призмы |
|---|---|---|
| Площадь основания | Определяет количество пространства, занимаемого призмой в плоскости основания | Чем больше площадь основания, тем выше может быть высота призмы |
| Объем | Выражает величину пространства, занимаемого призмой | Высота призмы зависит от объема и площади основания |
Примеры решения задач по определению высоты призмы
Далее представлены несколько примеров, в которых мы изучим способы определения высоты призмы. Каждая задача включает в себя уникальные условия, которые требуют применения соответствующих методов и формул.
| Задача | Условие | Решение |
|---|---|---|
| Пример 1 | Найдите высоту призмы, если известна площадь основания и объем: | Воспользуйтесь формулой для вычисления высоты призмы: |
| Пример 2 | Определите высоту прямоугольной призмы, зная длины ребер и площадь боковой поверхности: | Примените соответствующую формулу для рассчета высоты: |
| Пример 3 | Решите задачу, используя информацию о площади боковой поверхности и числе граней: | Изучите формулу, позволяющую определить высоту призмы: |
В каждом примере необходимо применить соответствующую формулу и метод, который позволит определить высоту призмы. Задачи имеют разные условия, что требует гибкого подхода и правильного выбора метода решения. Следуя данной методике, вы сможете успешно решать подобные задачи и укрепить свои навыки в области определения высоты призмы.
Алгоритм применения математических выкладок на практике с примерами

В данном разделе мы рассмотрим алгоритм использования математических формул на практике для определения высоты призмы. Математические выкладки позволяют нам решать различные задачи, связанные с геометрией и измерениями. На примере определения высоты призмы мы увидим, как правильный расчет и последовательность действий помогают нам получить точные результаты.
Шаг 1: Определение известных величин. Прежде чем использовать формулу для определения высоты призмы, необходимо точно знать значения других измерений, таких как площадь основания, объем или боковая поверхность. Данные величины могут быть известными или могут быть измерены с помощью линейки, штангенциркуля или других инструментов.
Шаг 2: Понимание формулы. Теперь, когда у нас есть известные величины, необходимо разобраться, как использовать соответствующую формулу для определения высоты призмы. Формула может быть простой или сложной, но основное понимание того, как применять ее, обеспечивает правильность расчетов.
Шаг 3: Подстановка значений и расчеты. Следующим шагом является подстановка известных величин в соответствующую формулу для вычисления высоты призмы. Важно следовать последовательности действий и правильно использовать операции, такие как умножение, деление, сложение и вычитание. Это обеспечивает точность ответа.
Пример: Допустим, у нас есть призма с площадью основания 36 квадратных сантиметров и объемом 108 кубических сантиметров. Чтобы найти высоту призмы, мы можем использовать формулу: высота = объем / площадь основания. Подставив значения в формулу, получим: высота = 108 / 36 = 3 сантиметра. Таким образом, высота призмы составляет 3 сантиметра.
Вопрос-ответ

Какую формулу использовать для определения высоты призмы?
Для определения высоты призмы используется формула: высота = объем / площадь основания.
Как узнать объем призмы?
Объем призмы можно узнать, умножив площадь основания на высоту.
Что делать, если не известна площадь основания призмы?
Если не известна площадь основания призмы, ее можно вычислить, зная стороны основания и используя соответствующую формулу (например, для прямоугольной призмы: площадь = длина * ширина).
Как найти площадь основания призмы?
Площадь основания призмы может быть найдена путем измерения сторон или радиуса основания и использования соответствующей формулы для его вычисления (например, для прямоугольной призмы: площадь = длина * ширина).
Какие еще способы существуют для определения высоты призмы?
Кроме формулы высоты, высоту призмы можно определить с помощью теоремы Пифагора или использовать метод подобия треугольников при известных соотношениях между сторонами призмы и другими фигурами.
Как определить высоту призмы?
Высоту призмы можно определить, используя формулу: h = V / S, где h - высота призмы, V - объем призмы, S - площадь основания призмы.
Что нужно знать, чтобы определить высоту призмы по формуле?
Для определения высоты призмы по формуле необходимо знать объем призмы (V) и площадь основания призмы (S).



