Нахождение аорты вектора может быть сравнено со сложной путешествией в поисках просветления. Магическое мгновение, когда все ваши усилия сходятся и ваши действия направлены по верному пути, аналогично нахождению аорты вектора. Выбор правильного метода и точный анализ данных играют решающую роль в достижении этой аорты и обеспечении успешности вашего исследования.
Именно в этой статье мы рассмотрим различные стратегии и приемы, которые помогут вам быстро и безошибочно найти ключевые элементы вектора. Мы изучим основные инструменты, аналитические подходы и методы обработки данных, которые помогут вам достичь величайшего потенциала в своих исследованиях и аналитических проектах.
Принципы определения главного направления вектора

В данном разделе рассматриваются основные принципы и методы определения главного направления вектора.
- Символ вектора, обозначающий его направление, позволяет ориентировать вектор в пространстве.
- Определение аорты вектора происходит путем определения его главного направления или направления максимальной величины.
- Одним из методов определения главного направления является анализ компонент вектора на оси координат.
- Другим методом является вычисление угла между вектором и определенной осью.
- Также можно использовать графические методы, такие как построение графика вектора и нахождение его направления с помощью инструментов и правил геометрии.
Важно отметить, что выбор метода определения главного направления вектора зависит от конкретной задачи и доступных инструментов. Эффективное определение главного направления вектора позволяет получить более точные результаты и увеличить точность анализа.
Знакомство с основополагающими понятиями

1. Вектор. Вектор является фундаментальным понятием векторного анализа и представляет собой направленную величину. Он обладает двумя основными характеристиками: направлением и длиной. Направление вектора задается в пространстве определенными углами относительно некоторых базисных величин, а его длина представляет собой числовое значение, характеризующее величину изменения.
2. Норма вектора. Норма вектора, также известная как его модуль или длина, определяется как евклидово расстояние от начала координат до конца вектора. Она представляет собой положительное число и играет важную роль при определении измеряемых величин и оценке масштабов изменений.
3. Единичный вектор. Единичный вектор имеет норму, равную 1. Он используется во множестве математических и физических задач, например, при задании направления движения или ориентации объектов в пространстве.
4. Компоненты вектора. Вектор может быть представлен как совокупность его компонентов, которые определяют его направление и величину вдоль каждой из координатных осей. Компоненты могут быть положительными или отрицательными, в зависимости от направления вектора.
Заключение. Ознакомление с базовыми понятиями векторного анализа является неотъемлемой частью изучения аорты вектора. Понимание и усвоение этих фундаментальных элементов позволит нам глубже проникнуть в суть исследуемой темы и более точно анализировать векторные характеристики.
Определение направления и размера вектора
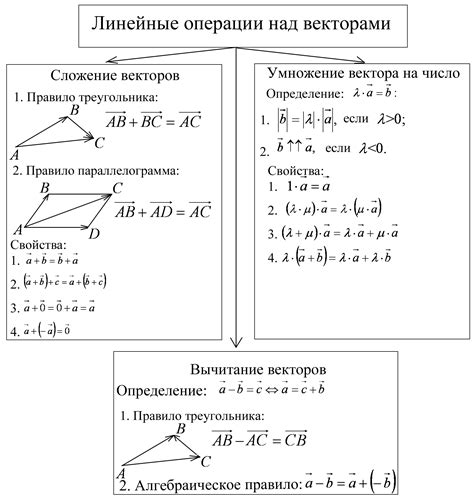
В данном разделе рассмотрим методы и приемы, которые позволят определить направление и размер вектора без необходимости использования специальных инструментов. Путем анализа геометрических и математических свойств вектора можно получить информацию о его ориентации и масштабе.
Определение направления
Для определения направления вектора можно воспользоваться его координатами или геометрическими свойствами. Если вектор задан в прямоугольной системе координат, то его направление можно найти, рассмотрев знаки его координат. Направление может быть положительным или отрицательным в зависимости от четверти, в которой находится вектор.
Также можно использовать геометрические приемы, такие как измерение угла между вектором и другими элементами, например, осями координат или другими векторами. Угол между векторами может помочь определить, направлены ли они в одну или противоположные стороны.
Определение размера
Размер вектора можно определить по его длине или модулю. Для вычисления длины вектора можно воспользоваться теоремой Пифагора или расстоянием между его начальной и конечной точками. Расстояние между точками можно найти, используя формулу, согласно которой каждая координата вектора возводится в квадрат, суммируется и извлекается квадратный корень.
Модуль вектора также позволяет определить его размер. Модуль вектора – это абсолютное значение его координат, игнорируя их направление. Модуль можно найти, применяя функцию модуля для каждой координаты и получив сумму абсолютных значений.
Улучшите точность и эффективность работы с векторами, используя методы определения направления и размера, которые были изложены в данном разделе.
Использование системы координат для определения направления главной оси векторного представления
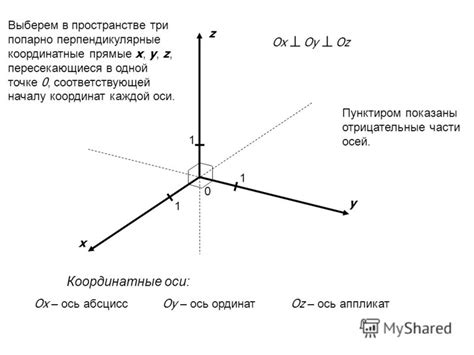
Для удобства визуализации и анализа координатной системы, рекомендуется использовать таблицу с двумя столбцами и тремя строками. В первом столбце размещаются значения координаты по оси, второй столбец описывает соответствующие значения пунктуации аорты.
| Значение координаты | Пунктуация аорты |
|---|---|
| Максимальное | Самый высокий уровень пунктуации аорты |
| Среднее | Средний уровень пунктуации аорты |
| Минимальное | Наименьший уровень пунктуации аорты |
Анализируя значения координаты и соответствующие пунктуации аорты, можно точно определить направление главной оси векторного представления, что позволит грамотно использовать эту информацию для дальнейших исследований и анализа данных.
Обзор алгоритмов поиска основного направления вектора

| Название алгоритма | Описание |
|---|---|
| Метод главных компонент | Метод, основанный на поиске главных компонент в пространстве векторов. Он находит основное направление вектора путем вычисления собственных значений и собственных векторов соответствующей ковариационной матрицы. |
| Алгоритм поиска максимального века | Алгоритм, который ищет направление вектора с максимальной нормой. Он выполняет итеративный процесс для нахождения наиболее значимого направления, основываясь на пороговом значении. |
| Алгоритм сингулярного разложения | Алгоритм, который использует сингулярное разложение матрицы векторов для нахождения основного направления. Он разлагает матрицу на три компоненты: левые и правые сингулярные векторы, а также сингулярные значения. |
Каждый из представленных алгоритмов имеет свои преимущества и недостатки, и выбор конкретного алгоритма зависит от требований исследования. Понимание различных методов поиска аорты вектора позволяет эффективно использовать и адаптировать их для конкретных задач и контекстов.
Изучение особых ситуаций при выявлении центрального направления вектора
В данном разделе рассмотрим нестандартные варианты, требующие особого подхода при определении главного вектора в заданном направлении. Мы изучим необычные сценарии, которые могут возникнуть в процессе поиска важного компонента вектора и предложим решения для достижения более точных результатов.
- Рассмотрение асимметричных форм
- Обнаружение аномалий в данных
- Учет изменений состояния окружающей среды
- Уточнение результатов при высокой степени шума
Каждый из этих случаев представляет определенные трудности для обычных методов поиска векторов и требует специализированного подхода. При изучении асимметричных форм, например, необходимо учитывать возможные аномалии и искать дополнительные указатели для определения наиболее точного направления.
Обнаружение аномалий в данных может помочь выявить скрытые особенности, которые могут повлиять на результаты поиска. Кроме того, учет изменений в окружающей среде может быть важным фактором при определении аорты вектора и требует дополнительного анализа.
Наконец, в случаях с высоким уровнем шума необходимо применять методы фильтрации, чтобы исключить нежелательные влияния на результаты. Это позволяет более точно определить главный вектор и получить надежные данные для дальнейшего анализа.
Применение методов для повышения точности определения направления главной оси вектора

В данном разделе рассматриваются различные приемы и техники, которые позволяют повысить точность определения направления главной оси вектора. Учитывая значение этого параметра в различных научных и инженерных областях, исследователи активно работают над разработкой более точных методов, устраняющих возможные искажения и ошибки в анализе.
Оптимизация алгоритмов: в данном контексте рассматриваются приемы оптимизации алгоритмов, основанные на повышении эффективности вычислительных процессов и уменьшении времени выполнения задач. Важными составляющими данного подхода являются учет особенностей конкретной задачи, оптимальный выбор математических моделей и алгоритмов обработки данных.
Избежание систематических ошибок: данный прием направлен на выявление и устранение возможных систематических ошибок при определении направления главной оси вектора. К систематическим ошибкам относятся искажения, связанные с инструментальной погрешностью, сложностью снятия экспериментальных данных и другими факторами, которые могут приводить к искажению конечного результата. Применение методов статистического анализа и корректировки значений позволяет уменьшить влияние систематических ошибок на точность определения направления.
Анализ неоднородностей: данный метод направлен на исследование неоднородностей векторных данных, которые могут возникать в процессе измерений. Существуют различные подходы и техники, позволяющие выявлять и корректировать неоднородности, такие как оценка сглаживания данных, исключение выбросов, адаптивная корректировка и другие. Анализ неоднородностей помогает повысить точность определения направления главной оси вектора за счет исключения погрешностей, связанных с неоднородностью данных.
Применение интеллектуальных алгоритмов: данный подход предназначен для применения интеллектуальных алгоритмов, таких как нейронные сети, генетические алгоритмы и алгоритмы машинного обучения, с целью повысить точность определения направления главной оси вектора. Использование этих методов позволяет автоматически выявлять закономерности в данных, оптимизировать параметры алгоритмов и повысить точность результатов.
Наконец, в последнем абзаце можно дать краткое заключение о значимости применения этих техник и их влиянии на точность определения направления главной оси вектора, подчеркнув их важность в различных научных и инженерных исследованиях.
Практические примеры выявления осязаемой центральной линии вектора
Одним из эффективных методов является использование проекций вектора на плоскость исследования. При данном подходе, проекция вектора на плоскость предоставляет информацию о его ориентации и направлении. Основываясь на результатах проекций, можно визуализировать аорту вектора и определить его центральную линию.
Другим распространенным методом определения аорты вектора является применение алгоритмов статистического анализа. Данный подход основывается на сборе и обработке данных, полученных в результате наблюдений или экспериментов с векторами. Статистический анализ позволяет вычислить различные параметры векторов и тем самым выделить осевую линию, наиболее точно отражающую их распределение.
Необходимо отметить, что каждый метод имеет свои преимущества и ограничения, которые следует учитывать при применении в конкретной ситуации. Выбор метода зависит от особенностей задачи, доступных данных и целей исследования. Использование различных методов определения аорты вектора может способствовать улучшению точности и скорости процесса анализа, сделав его более эффективным и надежным.
Вопрос-ответ

Какая точность можно достигнуть при поиске аорты вектора?
Поиск аорты вектора может быть выполнен с высокой точностью, зависящей от используемого метода. Например, при использовании компьютерного зрения и алгоритмов обработки изображений можно достичь точности в пределах нескольких пикселей.
Какие методы можно использовать для поиска аорты вектора?
Существует несколько методов для поиска аорты вектора. Некоторые из них включают использование компьютерного зрения, обработку изображений, анализ линий и текстур, а также алгоритмы машинного обучения.
Какую роль играет аорта вектор в компьютерном зрении?
Аорта вектор является важным элементом в компьютерном зрении, так как он позволяет определить направление объекта на изображении. Это помогает компьютеру распознавать и классифицировать объекты на основе их ориентации.
Какие сложности могут возникнуть при поиске аорты вектора?
При поиске аорты вектора могут возникнуть сложности, связанные с шумом на изображении, нечеткостью контуров объекта, а также с вариациями в текстурах и освещении. Однако современные методы компьютерного зрения и алгоритмы обработки изображений позволяют учесть и преодолеть эти сложности.
Какую пользу может принести точное определение аорты вектора?
Точное определение аорты вектора может иметь множество применений в разных областях. Например, в медицине это может помочь при диагностике сердечно-сосудистых заболеваний. В робототехнике точное определение аорты вектора может быть полезным для навигации и определения положения объектов. Автомобильная промышленность также может использовать эту информацию для оптимизации систем управления и безопасности.
Как можно быстро и точно найти аорту вектора?
Существует несколько методов для нахождения аорты вектора, которые позволяют получить результат быстро и с высокой точностью. Один из таких методов - это использование математических операций с векторами. Аорта вектора может быть найдена путем нахождения его направления и магнитуды. Для этого можно воспользоваться формулами и правилами, связанными с векторами, такими как правило параллелограмма или правило треугольника. Также можно использовать специализированные программы или алгоритмы, которые помогут выполнить эту задачу более точно и быстро.



