Иногда при решении математических задач встречается необходимость найти производную функции. Это важный инструмент, позволяющий выявить изменение функции в зависимости от ее аргумента. Однако, как найти эту производную? Как раскрыть тайну дифференцирования и узнать, как меняется функция? В данной статье мы погрузимся в мир математики и рассмотрим подробное объяснение процесса нахождения производной функции, а также приведем несколько примеров, чтобы лучше разобраться в этой теме.
Такой концепт, как производная функции, имеет свои особенности и интуитивно может показаться сложным. Однако, с помощью специальной формулы и некоторых математических операций мы можем раскрыть эту тайну и получить понимание о том, как меняется функция при изменении ее аргумента. В процессе дифференцирования мы ищем скорость изменения функции, то есть выясняем, как быстро значение функции меняется при изменении аргумента.
Существует несколько способов нахождения производной функции, но в данной статье мы рассмотрим одну из самых популярных формул - формулу первой производной. При использовании этой формулы мы сможем получить конкретное численное значение производной для любой функции. Разберемся подробнее, как работает эта формула и как ее применять на практике. Готовьтесь к великому погружению в мир математики и дифференцирования!
Основные понятия, которые необходимо изучить для понимания процесса нахождения производной функции

- Лимит функции: это понятие позволяет нам изучать поведение функции вблизи определенной точки. Он помогает определить, как значение функции меняется, когда ее аргумент приближается к определенному значению.
- Производная функции: это понятие выражает скорость изменения функции в зависимости от значения ее аргумента. Она позволяет нам определить наклон касательной к графику функции в заданной точке.
- Правила дифференцирования: существуют определенные правила, которые позволяют находить производные различных типов функций. Они помогают сократить процесс вычисления и упростить задачу.
- Дифференциал: это малое изменение значения функции, которое обусловлено малым изменением аргумента. Дифференциал является приближенным значением изменения функции и широко используется в дальнейших расчетах.
Изучение этих ключевых понятий поможет вам строить понимание процесса нахождения производной функции. Теперь давайте рассмотрим каждое понятие более подробно и приведем примеры их применения.
Применение производной к различным функциям
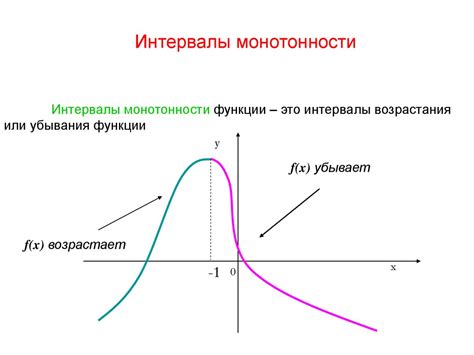
Рассмотрим несколько примеров для наглядного представления применения производной к разным типам функций. Во-первых, рассмотрим простейшую линейную функцию, которая представляет собой прямую линию графика. Производная такой функции будет постоянной величиной, определяющей угловой коэффициент наклона прямой.
Продолжим с более сложными функциями, такими как степенные и показательные функции. Применение производной к этим функциям позволяет определить, как изменяется их скорость роста или убывания в различных точках области определения.
Кроме того, рассмотрим случай тригонометрических функций, таких как синус и косинус. Применение производной к этим функциям позволяет определить максимальные и минимальные значения функций, а также точки, где функция имеет нулевую скорость изменения.
Описанные примеры лишь небольшая часть возможностей применения производной к различным функциям. Понимание этого инструмента позволяет более глубоко исследовать и анализировать функциональные зависимости и применять полученные знания в различных областях науки и инженерии.
Полезные советы для упрощения процесса вычисления производных

В данном разделе вы найдете полезные советы, которые помогут упростить процесс нахождения производной функции. Знание этих советов позволит вам более эффективно решать задачи, связанные с производными.
- Используйте свойства производной: получение производной суммы или разности функций, производной произведения или частного функций.
- Знайте основные формулы производных элементарных функций, таких как степенная функция, экспоненциальная функция, логарифмическая функция, тригонометрические функции.
- Применяйте правила дифференцирования сложных функций, таких как производная композиции функций, производная обратной функции.
- Используйте правила дифференцирования особых функций, таких как производная пограничных функций, производная неявно заданных функций.
- Не забывайте про правило Лейбница для произведения двух функций, которое позволяет упростить процесс нахождения производной.
- Имейте в виду, что приведение функции к виду, удобному для дифференцирования, может значительно упростить вычисление производной.
- Постоянно тренируйтесь на примерах, чтобы лучше понять и запомнить основные приемы нахождения производных.
Запомните эти советы и применяйте их в практике, и вы сможете более легко и быстро находить производные функций разных видов. Удачи в изучении производных!
Вопрос-ответ

Что такое производная функции?
Производная функции – это показатель изменения функции в каждой ее точке. Она позволяет определить скорость изменения значения функции по отношению к изменению аргумента.
Как найти производную функции?
Для нахождения производной функции можно использовать различные методы, включая формулу и правила дифференцирования. Формула для нахождения производной функции задается, как отношение приращения функции к приращению ее аргумента, предельно при стремлении приращения аргумента к нулю.



