В настоящее время, в эпоху цифровых технологий и информационного взрыва, анализ данных становится все более значимым и интересным. Его крайне важная роль в различных областях, от бизнеса до науки, ставит задачу разработки эффективных методов и моделей для извлечения информации из громадных объемов данных.
Одним из фундаментальных инструментов анализа данных является построение регрессионной модели. Эта задача заключается в нахождении зависимости между набором переменных с целью предсказания или объяснения значения одной из переменных на основе остальных.
Одним из наиболее популярных методов построения регрессионных моделей является использование линейной функции. Благодаря своей простоте и понятности, линейная регрессия применяется во многих областях, включая экономику, социальные науки, инженерию и многие другие.
В этой статье мы рассмотрим процесс построения регрессионной модели с помощью линейной функции, рассмотрим основные понятия и инструменты, необходимые для успешной работы с данным методом. Вы узнаете о ключевых шагах, начиная от обработки данных и выбора модели, до оценки ее качества и интерпретации результатов.
Основные концепции и принципы при разработке модели регрессии

В данном разделе мы рассмотрим ключевые понятия и принципы, которые лежат в основе построения регрессионной модели. Это поможет нам лучше понять процесс анализа данных и получения достоверных результатов.
- Целевая переменная: фактор, который мы хотим прогнозировать или объяснить с помощью наших независимых переменных.
- Независимые переменные: факторы, которые признаются потенциально влияющими на целевую переменную.
- Линейность: предполагается, что связь между независимыми переменными и целевой переменной является линейной. Это позволяет использовать линейную функцию для построения модели.
- Гипотеза: предположение о взаимосвязи между независимыми и зависимой переменными.
- Методы оценки: различные статистические методы используются для оценки параметров модели и определения степени их значимости.
- Residuals: разница между фактическими значениями целевой переменной и значениями, предсказанными моделью. Используется для оценки точности модели.
- Анализ мультиколлинеарности: процесс определения и устранения сильной корреляции между независимыми переменными, чтобы избежать искажения результатов.
Понимание этих концепций и принципов является важным шагом для успешного построения регрессионной модели. Использование линейной функции позволяет упростить моделирование, но требует тщательного анализа и интерпретации полученных результатов.
Основные свойства и применение линейной функции в моделировании

Одним из главных свойств линейной функции является пропорциональность между зависимой и независимыми переменными, что позволяет устанавливать прямую связь между ними. При этом, применение линейной функции позволяет аппроксимировать сложные зависимости между переменными и различными факторами.
Применение линейной функции в регрессионной модели позволяет не только выявить взаимосвязи между переменными, но и определить степень их влияния друг на друга. Использование соответствующих статистических методов и инструментов позволяет оценить значимость параметров и получить надежные предсказания.
- Линейная функция обладает свойством линейности, что позволяет устанавливать прямую связь между переменными и определить степень их зависимости.
- Применение линейной функции в регрессионной модели позволяет аппроксимировать сложные зависимости и извлекать ценную информацию из данных.
- Оценка параметров линейной функции с помощью статистических методов позволяет определить степень влияния каждой переменной на предсказываемую величину.
- Построение линейной регрессионной модели позволяет провести анализ и прогнозирование на основе имеющихся данных, что отражает важные свойства линейной функции.
В целом, линейная функция представляет собой мощный инструмент в моделировании и анализе данных, обладающий широким спектром свойств и применений в регрессионных моделях.
Выборка и предварительная обработка данных в анализе регрессии

Для построения адекватной регрессионной модели необходимо провести предварительную обработку выборки данных, которая будет использоваться в анализе. Этот процесс включает в себя несколько важных этапов, таких как сбор и организация данных, анализ выбросов и пропущенных значений, а также выбор подходящего метода обработки данных. Корректное выполнение этих шагов обеспечивает достоверные результаты моделирования и улучшает точность предсказаний.
С начала необходимо обеспечить надежность и качество данных, собранных для исследования. Это может включать в себя проверку методов сбора данных, и описание их надежности. Далее, следует провести анализ выбросов, чтобы определить и исключить аномальные наблюдения, которые могут исказить результаты анализа. Также стоит уделить внимание пропущенным значениям, которые могут возникнуть в данных, и принять решение о методе их обработки, например, заполнение или исключение.
Для более качественного представления данных и улучшения точности модели также может потребоваться выбор метода обработки данных. Это может включать в себя нормализацию, центрирование или стандартизацию данных. Каждый из этих методов имеет свои преимущества и применяется в зависимости от специфики данных и целей исследования. Например, нормализация данных может быть полезна, если переменные имеют разные единицы измерения и масштабы.
Таким образом, правильная предварительная обработка выборки данных является важным этапом в анализе регрессии. Она позволяет улучшить надежность и качество модели, а также повысить точность предсказаний и обеспечить более адекватные результаты исследования.
Математическая формулировка линейной регрессионной модели
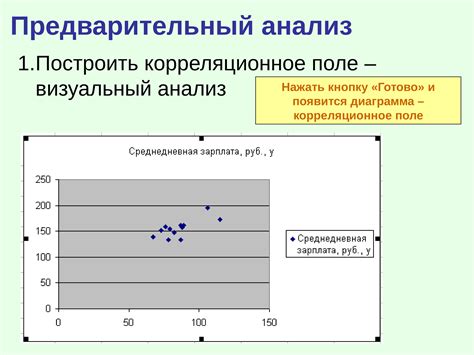
Этот раздел посвящен математической модели, которая позволяет анализировать зависимости между двумя переменными в виде прямой линии на плоскости. При помощи этой модели мы можем предсказывать значения одной переменной на основе значений другой переменной.
Математическая формулировка линейной регрессионной модели устанавливает, что изменение одной переменной ведет к пропорциональному изменению другой переменной. Она представляется уравнением прямой линии: y = mx + b, где y - зависимая переменная, x - независимая переменная, m - угловой коэффициент (наклон прямой) и b - свободный член (точка пересечения с осью y).
Данное уравнение позволяет нам построить линию, которая наилучшим образом описывает зависимость между переменными. Линейная регрессионная модель используется для аппроксимации данных и получения прогнозных значений.
Оценка параметров модели при помощи метода наименьших квадратов

В данном разделе будет рассмотрен метод оценки параметров регрессионной модели путем использования метода наименьших квадратов. Этот метод, основываясь на минимизации суммы квадратов отклонений между реальными значениями целевой переменной и предсказанными значениями модели, позволяет получить наилучшие оценки для параметров модели.
Для начала, давайте разберемся, что такое параметры модели и как они связаны с предсказываемой переменной. Параметры модели представляют собой коэффициенты, с помощью которых предсказываемая переменная связана с объясняющими переменными. Метод наименьших квадратов позволяет найти оптимальные значения для этих параметров таким образом, чтобы сумма квадратов отклонений между реальными и предсказанными значениями была минимальной.
Процесс оценки параметров модели с использованием метода наименьших квадратов состоит из нескольких шагов. Сначала необходимо сформулировать модель и определить функциональную зависимость между предсказываемой переменной и объясняющими переменными. Затем собираются данные по этим переменным и подбираются значения параметров таким образом, чтобы минимизировать сумму квадратов отклонений.
Метод наименьших квадратов широко используется в регрессионном анализе и является одним из наиболее распространенных методов оценки параметров модели. Он позволяет получить достоверные оценки и учитывает все доступные данные, уменьшая влияние случайных факторов на результат модели.
Вопрос-ответ

Какая роль линейной функции в построении регрессионной модели?
Линейная функция является базовой моделью для регрессионного анализа. Она позволяет описать связь между зависимой переменной и набором независимых переменных с помощью линейного уравнения. Такая модель является простой и понятной, легко интерпретируется и может быть использована для прогнозирования значений зависимой переменной.
В чем заключается суть построения регрессионной модели с помощью линейной функции?
При построении регрессионной модели с использованием линейной функции осуществляется аппроксимация зависимости между независимой переменной (X) и зависимой переменной (Y) с помощью линейного уравнения. Суть состоит в том, чтобы найти наилучшую прямую, которая лучше всего описывает данные и минимизирует сумму квадратов отклонений предсказанных значений от фактических.
Какие преимущества есть у линейной регрессионной модели?
Линейная регрессионная модель имеет несколько преимуществ. Во-первых, она является простой и понятной для интерпретации. Во-вторых, она позволяет оценивать влияние каждой независимой переменной на зависимую переменную. Кроме того, линейная модель может быть использована для прогнозирования значений зависимой переменной на основе известных значений независимых переменных.
Как определить качество построенной линейной регрессионной модели?
Оценка качества линейной регрессионной модели осуществляется при помощи различных статистических метрик. Наиболее распространенной является среднеквадратичная ошибка (Mean Squared Error - MSE), которая измеряет среднее значение квадрата отклонения между предсказанными и фактическими значениями. Также широко используется коэффициент детерминации (R-квадрат), который показывает, какую долю дисперсии в зависимой переменной можно объяснить с помощью независимых переменных модели.



