Представьте себе задачу, в которой вам необходимо определить все углы трапеции – одной из наиболее увлекательных геометрических фигур. И если вы думаете, что это миссия невыполнимая, мы рады вас разочаровать! В этой статье мы раскроем вам простую и интуитивно понятную методику, которая поможет вам легко и точно определить все углы трапеции без особых усилий.
Давайте разберемся, что такое трапеция. Трапеция – это четырехугольник с двумя параллельными сторонами. А вот что интересно: нет необходимости знать все определения и формулы геометрии, чтобы найти углы трапеции! Мы предлагаем вам более простой и интуитивный подход, основанный на измерении сторон и средней линии этой фигуры.
В процессе нашего исследования мы поняли, что секрет нахождения углов трапеции кроется не только в измерении длин сторон, но и в определении ее средней линии. С помощью этой простой методики, основанной на хитрой комбинации измерений и математических операций, вы сможете добраться до желаемых результатов в кратчайшие сроки и безо всякого фрустрирующего временного и энергетического затрат.
Особенности и определение трапеции

Рассматривая геометрию фигур, необходимо уделять внимание таким специальным многоугольникам, как трапеции. Они обладают определенными особенностями и характеристиками, которые могут быть полезными при решении геометрических задач.
Трапеция - это четырехугольник, у которого две противоположные стороны параллельны. Особенностью трапеции является то, что она имеет две основания - длинное и короткое, которые расположены на противоположных концах фигуры. Остальные две стороны называются боковыми.
Трапеции могут быть различных видов в зависимости от угловых характеристик, например, прямоугольная, равнобедренная или общего вида. Каждый вид трапеции обладает своими особенностями, специальными свойствами и формулами для вычисления площади и других параметров.
Изучение особенностей и характеристик трапеций может быть полезным для решения задач по геометрии, таких как нахождение углов, сторон или площади трапеции. Поэтому основное знание об определении и свойствах трапеций является необходимым для успешного решения таких задач.
Описание основных характеристик фигуры с параллельными основаниями

Свойства и особенности трапеции
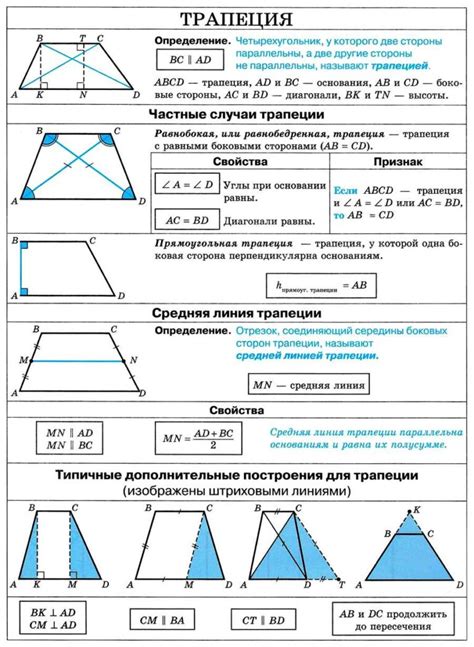
Кроме того, одним из важных свойств трапеции является равенство углов при основаниях. Таким образом, углы между боковыми сторонами и основаниями будут равными углами, что важно учитывать при изучении данной геометрической фигуры.
Трапеция также обладает свойством суммы внутренних углов, равной 360 градусам. Каждый из углов трапеции вносит свой вклад в эту сумму, и исследование их величин позволяет получить полное представление о форме и углах данной фигуры.
Наличие параллельных сторон делает трапецию похожей на параллелограмм, однако их различие заключается в отсутствии равных противоположных сторон. Трапеция может иметь различные формы и размеры, но она всегда остается фигурой с двумя параллельными сторонами и двумя непараллельными.
Как определить углы трапеции по измерениям ее боковых сторон?
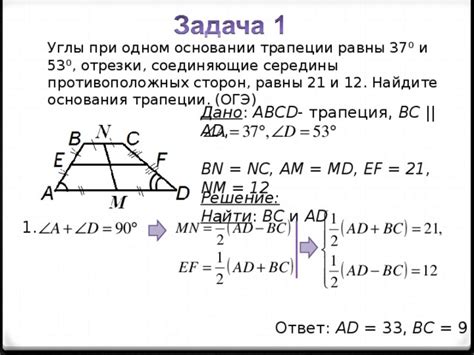
При решении геометрических задач важно уметь определить углы фигур по измерениям их сторон. В данном разделе мы рассмотрим простую методику для нахождения углов трапеции на основе известных длин ее боковых сторон. Подобный подход позволяет избежать излишнего использования сложных формул и обеспечивает быстрое решение задачи.
Общие принципы формул для определения углов трапеции
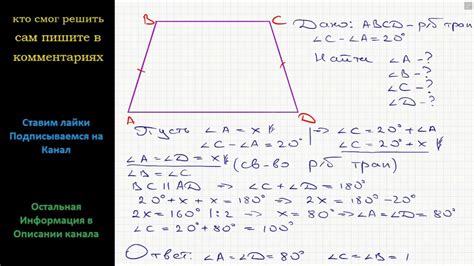
В данном разделе будет рассмотрена методика вычисления углов трапеции на основе заданных сторон и средней линии. Объяснены будут основные принципы и формулы, которые позволяют определить значения углов данной геометрической фигуры с использованием различных параметров.
Для вычисления углов трапеции существует несколько подходов, но все они основаны на известных свойствах этой фигуры. Важно отметить, что трапеция имеет параллельные стороны и две непараллельные стороны, называемые основаниями. Величины этих оснований и средней линии являются ключевыми параметрами, по которым можно определить значения углов.
Для начала, стоит подчеркнуть важность знания длины сторон трапеции и значения средней линии. Длина оснований и средней линии могут быть представлены разными способами, но наиболее часто встречающимся является использование метрической системы. В результате, значения оснований и средней линии будут выражены в метрах, сантиметрах или других подобных единицах измерения.
Далее, на основе известных значений оснований и средней линии трапеции, можно использовать различные формулы для определения углов. Одна из самых распространенных формул основана на теореме косинусов и позволяет найти углы трапеции, зная значения сторон и средней линии.
Решение задач по определению углов трапеции: простые примеры
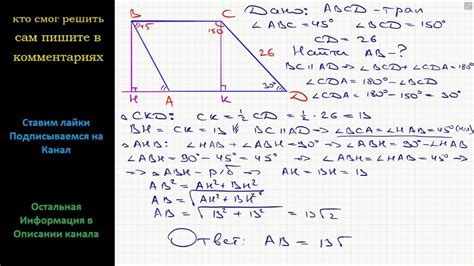
В данном разделе представлены примеры задач, связанных с определением углов трапеции. Мы рассмотрим несколько ситуаций, в которых необходимо найти значения углов, используя известные стороны и информацию о средней линии.
| Пример задачи | Решение |
|---|---|
| Задача 1 | Дана трапеция ABCD, в которой AB |



