В мире геометрии существует великое множество фигур, каждая из которых обладает своей уникальной красотой и интригующими характеристиками. Одной из таких фигур является трапеция - двухосновная фигура, которая порождает ощущение гармонии и стабильности благодаря своим параллельным основаниям. Однако, это только вершина айсберга, истинная загадка трапеции заключается в определении ее высоты по известным основаниям.
Если обратиться к мудрости древних математиков, то можно открыть перед собой алгоритмический лабиринт, который приведет к ответу на вопрос, куда направить свой взгляд для разгадки тайны высоты трапеции. Разумеется, это далеко не простая задача, и требуется время, сознательность и усидчивость для постижения этого искусства. Но именно в этом кроется его прелесть - постижение глубин математического мира и умение решать сложные задачи.
Чтобы сделать первый шаг в понимании тонких нюансов вычисления высоты трапеции, необходимо обратиться к ее суть. Высота трапеции - это отрезок, проведенный перпендикулярно между ее основаниями, который не только делит фигуру на две равные части, но и позволяет раскрыть ее геометрические свойства. Чтобы определить его длину, следует обратить внимание на различные элементы трапеции, такие как углы и длины сторон, а также использовать некоторые хитрости и формулы, которые были открыты гениальными умами математиков давно, но до сих пор не потеряли своей актуальности и значимости.
Методы и принципы определения высоты трапеции: изучение основных подходов
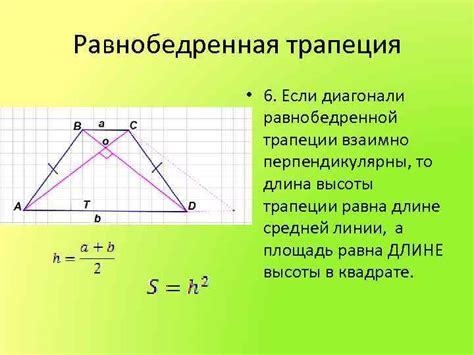
Существуют несколько подходов к определению высоты трапеции. Один из наиболее распространенных методов основан на использовании свойства, согласно которому высота трапеции является перпендикулярной линией, проведенной от одного основания к противоположной его точке на другом основании.
Другой метод, который также широко применяется, основан на использовании формулы для площади трапеции. При известных значениях оснований и площади трапеции можно использовать данную формулу для определения высоты. Обратная операция также возможна: если известны значения оснований и высоты, можно вычислить площадь трапеции.
Метод рассечения трапеции на два треугольника также может быть полезным при определении её высоты. Путем проведения линии, соединяющей медианы на параллельных сторонах трапеции, можно получить два треугольника, в одном из которых высота будет прямоугольной линией. Известная формула для высоты треугольника может быть использована для определения высоты трапеции.
В данном разделе мы рассмотрели основные методы и принципы определения высоты трапеции, а также ознакомились с несколькими подходами, используемыми в геометрии. Применение этих методов позволяет более точно измерять параметры трапеции и использовать их при проведении дальнейших вычислений и анализе геометрических фигур.
Понятие трапеции и ее основания
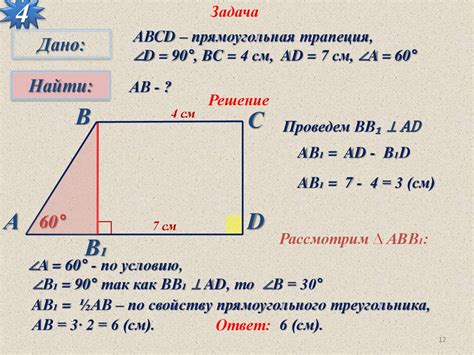
Когда мы говорим об основаниях трапеции, мы имеем в виду ее две параллельные стороны. Одно из оснований обычно называется большим, а второе - меньшим. На основаниях трапеции мы можем строить различные прямые линии и отрезки, включая высоту.
Высота трапеции - это перпендикуляр, опущенный из вершины трапеции на основание. Она является заметной характеристикой трапеции, поскольку определение высоты позволяет решать различные задачи в геометрии. Определение высоты трапеции может быть полезным, например, при рассмотрении площади трапеции или при нахождении длины боковой стороны.
Теперь, когда мы уточнили понятие трапеции и основания, мы можем перейти к методам определения высоты на базе известных оснований. Решение этой задачи связано с использованием геометрических формул и связей между сторонами и углами трапеции.
Применение специальной формулы для расчета высоты трапеции
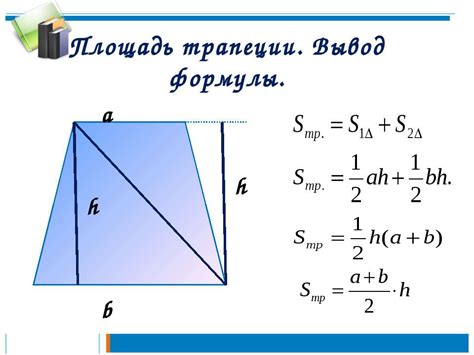
В данном разделе рассмотрим один из методов определения высоты трапеции, основываясь на использовании специальной формулы. Этот метод позволяет вычислить значение высоты, исходя из известных параметров трапеции без необходимости проведения дополнительных измерений или использования других формул.
Предлагаемый метод основан на использовании формулы, специально разработанной для расчета высоты трапеции. Эта формула учитывает величины оснований и других известных параметров, позволяя определить значение высоты без необходимости проведения сложных геометрических операций.
Для применения этого метода необходимо знать длины обоих оснований трапеции и, возможно, другие известные параметры, такие как углы, длины боковых сторон или диагоналей. Используя значения этих параметров, мы можем подставить их в формулу и получить результат – высоту трапеции.
Таким образом, использование специальной формулы для расчета высоты трапеции предоставляет удобный и эффективный способ определить данное значение без лишних измерений или сложных вычислений. Этот метод особенно полезен в практических задачах, связанных с геометрией и строительством, где требуется быстрый и точный расчет высоты трапеции по известным параметрам.
Метод 2: Измерение высоты с помощью треугольника и теоремы Пифагора
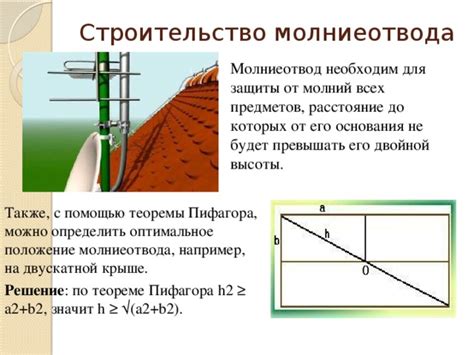
В данном разделе рассмотрим второй метод определения высоты трапеции. Для этого мы воспользуемся треугольником и известной нам теоремой Пифагора.
Идея этого метода заключается в том, чтобы создать прямоугольный треугольник на основании трапеции с известной высотой. Затем, применяя теорему Пифагора, мы сможем вычислить неизвестную нам высоту.
Для начала, отметим выбранную нами высоту трапеции на одном из ее оснований и соединим получившиеся точки с вершинами противоположного основания. Таким образом, мы получим прямоугольный треугольник, в котором известны два катета - высота трапеции и одно из оснований.
Применяя теорему Пифагора, которая утверждает, что квадрат гипотенузы треугольника равен сумме квадратов его катетов, мы можем вычислить длину неизвестной нам высоты. Просто подставьте известные значения в формулу и найдите неизвестное значение.
Таким образом, метод 2 предлагает использовать прямоугольный треугольник и теорему Пифагора для определения высоты трапеции по известным основаниям. Этот метод является эффективным и точным способом решения данной задачи.
Метод 3: Применение подобных фигур и пропорций для вычисления высоты трапеции
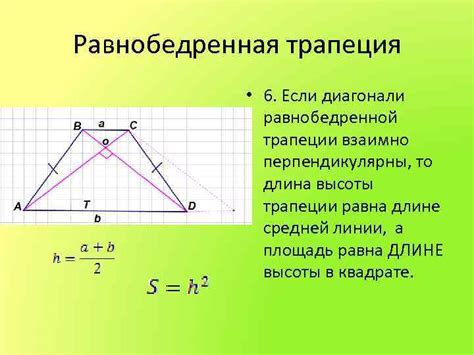
Для начала, нам потребуется рассмотреть подобные фигуры, которые имеют одинаковые формы, но различаются в размерах. Затем, мы можем использовать пропорции между соответствующими сторонами этих подобных фигур, чтобы найти искомую высоту трапеции.
Для применения этого метода, мы можем воспользоваться формулой: h = ((b2 - b1) * H1) / (B1 - B2), где h - искомая высота трапеции, b1 и b2 - длины оснований, H1 - длина высоты подобной фигуры соответствующего основания b1, B1 и B2 - длины оснований соответственно для двух подобных фигур.
| Известные параметры | Подобные фигуры |
|---|---|
| Длина основания b1 | Длина основания B1 |
| Длина основания b2 | Длина основания B2 |
| Длина высоты H1 | Искомая высота h |
Выбирая подходящие значения для b1, b2, B1, B2 и H1, мы можем подставить их в формулу и получить искомое значение высоты трапеции. Однако, важно учитывать правильность определения подобных фигур и точности измерений, чтобы получить верный результат.
Выбор наиболее удобного способа вычисления высоты трапеции
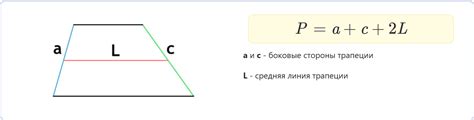
При определении высоты трапеции, можно применять различные методы, которые позволяют получить точные и надежные результаты. Выбор наиболее удобного способа зависит от основных параметров и условий задачи, а также от предпочтений и опыта пользователя.
Существует несколько методов, позволяющих определить высоту трапеции. В одном из них используется геометрическая формула, основанная на известных значениях оснований и угле, образованном диагоналями, в результате чего можно вычислить высоту. Этот метод позволяет получить точные результаты, но требует знания геометрических принципов и решения уравнений.
Другой способ основывается на использовании тригонометрических функций и известных значениях оснований и угла наклона трапеции. Путем применения соответствующих тригонометрических формул, можно определить высоту с помощью известных данных. Этот метод требует знаний тригонометрических функций и умения применять их в задачах геометрии.
Кроме того, существуют методы, основанные на использовании подобия треугольников или применении теоремы Пифагора. Эти методы позволяют вычислить высоту трапеции с использованием соотношений между сторонами и углами. Они могут быть удобными в определенных ситуациях, так как не требуют сложных математических выкладок.
Важно учитывать характеристики конкретной задачи и уровень подготовки пользователя при выборе наиболее удобного способа определения высоты трапеции. Рекомендуется ознакомиться с различными методами и найти тот, который наиболее подходит для конкретной ситуации. В случае возникновения затруднений, всегда можно обратиться к учебным пособиям или консультации с учителем, чтобы получить дополнительную помощь и разъяснения.
Вопрос-ответ

Как определить высоту трапеции по известным основаниям?
Высота трапеции может быть определена с использованием формулы площади трапеции. Площадь трапеции равна половине произведения суммы ее оснований на ее высоту. Исходя из этой формулы, высоту можно выразить как отношение площади трапеции к произведению оснований.
Можно ли определить высоту трапеции только по ее основаниям?
Да, высоту трапеции можно определить только по ее основаниям. Для этого нужно использовать формулу площади трапеции, в которой высота выражается через известные основания.
Какая формула позволяет определить высоту трапеции?
Формула для определения высоты трапеции выглядит следующим образом: высота равна площади трапеции, деленной на половину суммы ее оснований. Эта формула позволяет определить высоту только по известным основаниям.
Если известны только длины оснований, можно ли определить высоту трапеции?
Да, если известны только длины оснований, можно определить высоту трапеции. Для этого используется формула, в которой высота выражается через известные основания и площадь трапеции.
Есть ли другие способы определить высоту трапеции?
Другие способы определения высоты трапеции с использованием только известных оснований могут быть достаточно сложными и требовать дополнительных данных. Однако, при известной площади трапеции, можно использовать формулу, выражающую высоту через основания и площадь.
Как определить высоту трапеции, если известны длины обоих оснований?
Для определения высоты трапеции по известным длинам обоих оснований необходимо использовать формулу: высота = (2 * площадь) / (сумма длин оснований). Сначала нужно найти площадь трапеции, умножив сумму длин оснований на высоту и разделив на 2. Затем, используя найденную площадь и сумму длин оснований, подставьте значения в формулу, чтобы определить высоту.



