Даже самые совершенные функции имеют своеобразные "подводные камни", которые могут привести к появлению точек разрыва. На первый взгляд может показаться, что нахождение таких точек является сложной задачей, требующей много времени и усилий. Однако, при использовании определенных методов и контрольных приемов, поиск этих мест становится более удобным и легким.
Для начала важно отметить, что точки разрыва функции могут возникать по разным причинам. Некоторые из них связаны с неопределенностью или отсутствием предела в определенных точках, в то время как другие могут возникать из-за несоответствия значений функции в определенных интервалах. Понимание этих различий позволяет нам более эффективно искать и распознавать точки разрыва.
Для установления наличия точек разрыва функции необходимо использовать специальные методы, которые позволяют анализировать ее поведение в различных точках и интервалах. Некоторые из этих методов включают анализ графика функции, исследование ее асимптотического поведения и проверку на существование пределов на границах различных интервалов. Каждый из этих методов имеет свои особенности и может быть эффективным в определенных ситуациях, поэтому рекомендуется применять все доступные приемы для нахождения точек разрыва функции.
Как формируются и возникают точки разрыва в функциях?

Когда мы говорим о точках разрыва функции, мы обращаем внимание на особые моменты, когда функция теряет свою непрерывность и ее график не может быть нарисован в одной непрерывной линии. Эти точки представляют собой переломные моменты, где функция ведет себя иначе, меняя направление или значения.
Одна из основных причин возникновения точек разрыва - это нарушение определения функции в некоторых точках области определения. Это может происходить, например, из-за деления на ноль или применения функции, которая не имеет определения в этой точке, такой как квадратный корень из отрицательного числа.
Точки разрыва могут вызываться и другими факторами, такими как расхождение графика функции на разные ветви, пересечение с асимптотами, наличие вертикальных, горизонтальных или изломовых асимптот. Эти факторы могут изменять поведение графика функции и создавать особые точки.
| К примеру, | на графике функции y = 1/x, можно наблюдать точку разрыва в x=0. В этой точке график функции имеет вертикальную асимптоту и меняет свое направление с положительного на отрицательное. |
| Также, | функция y = |x| имеет точку разрыва в x=0. В этой точке происходит смена знака функции и график имеет излом, меняя свое направление. |
Точки разрыва являются важными концепциями, которые помогают понять поведение функций и определить их особенности. При анализе функций и их графиков, поиск, понимание и классификация точек разрыва может быть полезным инструментом для изучения и описания функциональных зависимостей.
Различия между точками разрыва и точками разрыва первого рода

- Точки разрыва: важные точки, где функция перестает быть непрерывной и имеет необычное поведение. Здесь функция может иметь различные виды разрывов, которые будут рассмотрены далее.
- Точки разрыва первого рода: особые случаи точек разрыва, которые описываются в терминах пределов функции. В таких точках пределы функции справа и слева существуют, но они не равны друг другу.
Точка разрыва может быть как точкой разрыва первого рода, так и другим видом разрыва, который будет рассмотрен далее. Важно отличать такие случаи, так как они требуют различного подхода к их анализу.
В точках разрыва первого рода пределы функции могут стремиться к разным значениям, что приводит к неопределенности. Это означает, что функция имеет раздельные пределы справа и слева от точки разрыва первого рода.
Важно понимать различия между точками разрыва и точками разрыва первого рода, чтобы правильно классифицировать и изучать особенности функции в этих точках. Это поможет нам углубить наше понимание и лучше анализировать их в контексте изучения точек разрыва функции.
Особенные функции с периодическими прерываниями в виде точек разрыва
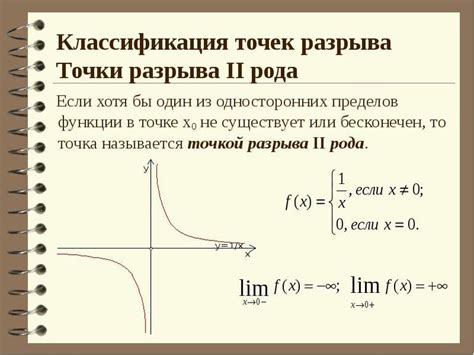
Примером такой функции может служить модуль функции, который описывает расстояние от точки до начала координат. В точке разрыва функция меняет свое направление, что делает ее непрерывной на всем ее определенном интервале, однако скачком меняет свое значение. Именно в таких точках, где происходит скачок, можно найти точки разрыва.
Другим примером функции с точками разрыва может быть гиперболический тангенс, который принимает значение бесконечности в точках разрыва. Функция имеет асимптоты на протяжении всего определенного интервала, но в точках разрыва значительно изменяет свое поведение.
Раскрытие приемов обнаружения точек разрыва функции

Закономерности в функциональных разрывах, которые возникают при анализе определенных функций, могут быть выявлены с использованием различных методов и приемов. В данном разделе мы рассмотрим несколько эффективных стратегий для обнаружения точек разрыва функций и понимания их характеристик.
| Метод | Описание |
|---|---|
| Анализ знаменателя | Один из наиболее распространенных подходов, основанный на анализе знаменателя функции. Начинается с выявления точек, где знаменатель обращается в ноль, так как это типичная причина возникновения разрывов функций. |
| Исследование пределов | Другой метод основан на анализе пределов функции по обеим сторонам точки, которая может быть потенциальной точкой разрыва. Изучение поведения функции вблизи этих пределов позволяет определить, является ли точка разрывом или нет. |
| Анализ графика | Этот метод включает в себя построение графика функции и визуальное обнаружение возможных точек разрыва. Он основывается на знании различных типов разрывов и их проявления на графике функции. |
| Применение дифференциального исчисления | Дифференциальное исчисление может быть полезным инструментом при поиске точек разрыва функций. Анализ производных позволяет выявить особенности функции и определить возможные точки разрыва. |
Каждый из этих методов имеет свои преимущества и ограничения, и часто их комбинирование приводит к наиболее точным и надежным результатам при обнаружении точек разрыва функции. Усвоение всех этих приемов позволит легко находить и понимать характеристики разрывов на графиках функций, что является важным навыком для изучения и анализа математических моделей и приложений.
Анализ графика функции: методы изучения изменений в поведении функции
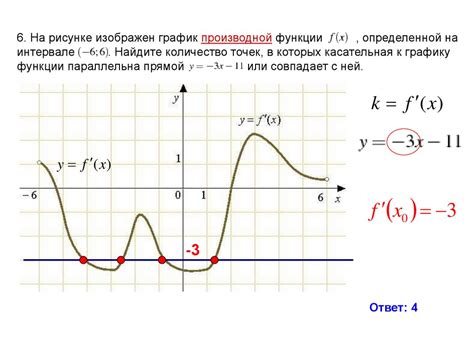
Погружаясь в глубины анализа графика функции, мы раскрываем удивительный мир ее поведения. Различные методы и подходы позволяют нам узнать больше о точках перегиба, экстремумах или особых характеристиках функции без использования конкретных математических определений.
Один из наиболее эффективных методов анализа графика функции - это визуальное изучение его формы и особенностей. Различные формы графика, такие как волны, локти, пики и ямы, указывают на различия в поведении функции в разных участках своего пространства определения. Более высокие или нижние значения функции могут указывать на точки перегиба или экстремумы, которые исследователь может узнать, не вдаваясь в математические выкладки.
Вторым важным методом является анализ производной функции. Производная функции позволяет нам определить моменты, когда функция изменяет свое поведение. Различия в производной могут указывать на точки разрыва функции, области роста и убывания, а также ее скорость изменения. Используя методы дифференцирования и решения уравнений, исследователь может определить точные значения этих характеристик функции.
Третий метод представлен анализом асимптотического поведения функции. Асимптоты делают невидимые части графика функции видимыми, указывая на границы поведения функции в бесконечности. Вертикальные асимптоты указывают на точки разрыва, горизонтальные на области стабильности или роста. Знание об асимптотах позволяет лучше понять, как функция ведет себя вне своей определенной области.
- Визуальный анализ формы графика функции;
- Анализ производной функции и ее изменений;
- Анализ асимптотического поведения функции.
Анализ особых моментов функции
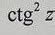
В данном разделе мы рассмотрим методы и подходы к анализу особых точек функции. Отдельные точки функции могут отличаться от общего хода графика и иметь особое значение в контексте ее поведения. Путем анализа таких особых точек мы сможем получить более глубокое понимание функции и ее характеристик.
Первым методом анализа является изучение точек разрыва функции. Они представляют собой значения x, в которых функция обнаруживает разрыв в своей непрерывности. Такие разрывы могут быть вызваны различными факторами, например, различными определениями функции на разных участках графика или нарушением непрерывности в одной точке графика.
Кроме точек разрыва, в анализе функции важными являются также точки разрыва первого и второго рода. Точками разрыва первого рода называются значения x, в которых функция имеет разрыв только в одной из сторон, например, слева или справа. Такие точки могут быть вызваны различными математическими особенностями функции, например, делением на ноль или несуществованием предела.
Точками разрыва второго рода называются значения x, в которых функция имеет разрыв и слева, и справа. Такие точки являются особыми и могут быть вызваны, например, изломами в функциональной зависимости или точками изолированного разрыва.
- Метод анализа точек разрыва функции
- Метод анализа точек разрыва первого рода
- Метод анализа точек разрыва второго рода
Таким образом, анализ особых точек функции является важным шагом в изучении ее свойств и характеристик. Поиск, исследование и классификация таких точек помогут нам получить более полное представление о функции и ее поведении в разных участках графика.
Метод вычисления границ функции в окрестности потенциальных точек разрыва

Рассмотрим способы определения пределов функции вблизи точек, обладающих потенциальными разрывами. При анализе данных точек необходимо использовать методы, которые позволят найти верхнюю и нижнюю границы функции для близлежащих значений.
Один из эффективных методов для расчета пределов - метод дробления знаменателя. Суть метода заключается в разложении выражения функции на два слагаемых таким образом, чтобы одно из них содержало потенциальное значение разрыва и имело значение нуля в этой точке. Затем, применяется алгебраический прием, который позволяет упростить исходное выражение и вычислить численное значение предела для обеих частей выражения.
Еще одним методом является асимптотическое приближение. Оно используется для определения пределов функции путем поиска асимптотических кривых, которые приближают поведение функции вблизи точек разрыва. Определение асимптотических кривых позволяет найти верхние и нижние границы функции в окрестности потенциальных точек разрыва.
Еще одним подходом является применение метода Лопиталя. Он предоставляет возможность рассчитать предел функции в точках разрыва путем нахождения предела отношения производных функции и производной самой функции. Этот метод позволяет определить предельное значение функции для сложных случаев, когда другие методы могут не давать однозначного результата.
- Метод дробления знаменателя
- Асимптотическое приближение
- Метод Лопиталя
Расчет пределов функции в окрестности потенциальных точек разрыва позволяет более полно описать поведение функции и выявить особенности приближения к возможным разрывам. Использование различных методов позволяет получить более точные и достоверные результаты, учитывая конкретные условия и свойства функции.
Вопрос-ответ

Какие методы существуют для нахождения точек разрыва функции?
Для нахождения точек разрыва функции существуют несколько методов. Один из них - метод анализа графика функции. Он основывается на том, что разрывы функции могут возникать в точках, где график функции имеет особенности, такие как разрывы, разрывы первого рода (скачки) или разрывы второго рода (асимптоты).
Как определить точки разрыва функции по определению?
Точка разрыва функции определяется по определению, если хотя бы одно из следующих условий выполняется: 1) функция не определена в данной точке; 2) функция имеет бесконечное значение в данной точке; 3) предел функции в данной точке не существует или не равен значению функции в этой точке.
Приведите примеры функций с точками разрыва разных видов.
Примеры функций с точками разрыва разных видов могут быть следующими: 1) функция с разрывом первого рода, например, f(x) = 1/x, которая имеет скачок при x = 0; 2) функция с разрывом второго рода, например, f(x) = 1/sin(x), которая имеет вертикальную асимптоту при x = kπ, где k - целое число; 3) функция, которая не определена в некоторых точках, например, f(x) = √(x-1) - функция не определена при x ≤ 1.
Какой график может быть у функции с разрывом первого рода?
График функции с разрывом первого рода может иметь вид двух отдельных частей, между которыми есть пропуск или "скачок". Например, график функции f(x) = 1/x будет иметь две разные части: одну, при x > 0, и вторую, при xКак определить точки разрыва функции с помощью пределов?
Для определения точек разрыва функции с помощью пределов необходимо проверить, существуют ли пределы функции слева и справа от данной точки и равны ли они значениям функции в этой точке. Если пределы существуют и равны значению функции, то точка не является точкой разрыва. Если хотя бы один из пределов не существует или не равен значению функции, то точка будет являться точкой разрыва.Какие методы можно использовать для нахождения точек разрыва функции?
Для нахождения точек разрыва функции можно использовать несколько методов. Один из них - анализ знаков функции на интервалах. Если функция меняет знак между двумя интервалами, то возможно на границе этих интервалов находится точка разрыва. Еще один метод - анализ поведения функции около потенциальной точки разрыва. Если функция не имеет предела или имеет разные лимиты слева и справа от точки, то это может быть точка разрыва. Также можно использовать методы математического анализа, например, дифференциальное исчисление, для нахождения точек разрыва.



