Когда мы говорим о треугольнике, у нас сразу возникают ассоциации с самыми разными понятиями: углы, стороны, высоты. Но как насчет некого "радиуса", который, по неизвестным причинам, остается в тени и не привлекает к себе особой внимания? Несмотря на свою скромность, радиус вписанной окружности играет важную роль и имеет своеобразную связь с другими элементами треугольника.
Представьте ситуацию, когда вы хотите узнать, насколько близко связаны между собой вершины треугольника. Вот где на помощь приходит радиус вписанной окружности! У этого загадочного понятия есть способность объединять все вершины треугольника, будто бы "оглавливая" их. При этом, радиус остается внутри фигуры, что является еще одной загадкой, стоящей перед исследователями геометрии.
Когда мы говорим о радиусе, на помощь приходит еще одно чудо геометрии - вписанная окружность. Это особая окружность, которая наиболее тесно укладывается внутри треугольника, касаясь каждой из его сторон. Именно окружность становится отправной точкой для изучения радиуса вписанной окружности и его связи с остальными частями треугольника.
Сущность и особенности радиуса инкруга

Основное свойство радиуса инкруга в треугольнике заключается в том, что он всегда перпендикулярен к стороне треугольника и делит ее на две равные части. Это означает, что центр инкруга совпадает с точкой пересечения трех биссектрис треугольника.
Радиус инкруга является важным параметром, так как от него зависят другие свойства и характеристики треугольника. Например, радиус инкруга с помощью формулы Эйлера связан с радиусом описанной окружности и расстоянием от центра инкруга до центра описанной окружности. Этот связанный радиус раскрывает дополнительные характеристики треугольника, такие как его площадь и стороны.
Описание особенности внутренней окружности в треугольнике
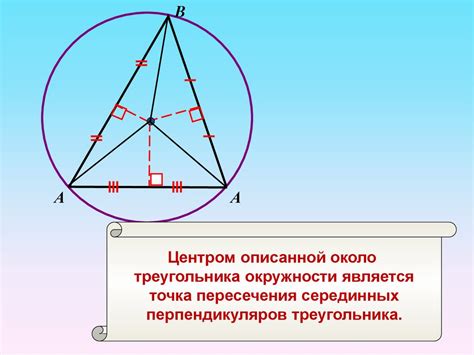
Внутренняя окружность, еще называемая описанной окружностью, является особенным элементом в треугольнике. Этот круг вписан точно внутрь треугольника, касаясь всех его сторон. Радиус вписанной окружности определяет насколько близко она находится к вершинам треугольника, то есть величину ее радиуса.
В зависимости от размеров сторон и углов треугольника, радиус вписанной окружности может быть разным. Он имеет особую важность в геометрии, так как связан с другими параметрами треугольника. Например, он является половиной длины суммы радиусов описанных окружностей вокруг каждого из внутренних углов треугольника.
- Радиус вписанной окружности также может быть выражен через площадь треугольника и его полупериметр. Найдя площадь треугольника по формуле Герона и полупериметр, можно легко определить радиус вписанной окружности.
- Чем ближе стороны треугольника к равенству, тем больше радиус вписанной окружности.
- Радиус вписанной окружности также связан с расстояниями от вершин треугольника до центра окружности.
Изучение радиуса вписанной окружности полезно для понимания геометрических свойств треугольников и дальнейшего исследования их различных параметров. При анализе треугольников, важно учитывать и изучать связь радиуса вписанной окружности с другими характеристиками этой фигуры.
Свойства центральной окружности треугольника
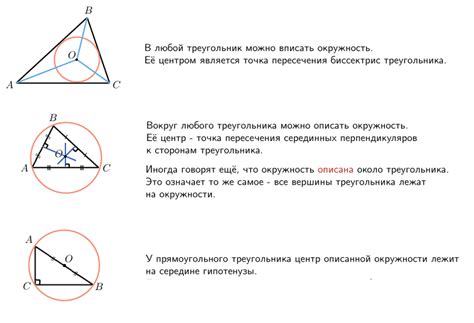
Одно из главных свойств центральной окружности треугольника - это то, что радиус этой окружности является пересекающимся перпендикуляром ко всем сторонам треугольника. Иными словами, если мы проведем радиусы из центра окружности к серединам каждой из сторон треугольника, то эти радиусы будут перпендикулярны к соответствующим сторонам. Это свойство радиуса позволяет уведомить нас о его уникальной роли в треугольнике и его значения можно использовать для нахождения других величин и углов.
Еще одно важное свойство радиуса центральной окружности треугольника - это то, что он равен половине радиуса описанной окружности, которая проходит через вершины треугольника. Зная значения радиусов обеих окружностей, мы можем рассчитать различные параметры треугольника, такие как его площадь, периметр и углы.
Кроме того, радиус центральной окружности треугольника связан с ориентацией треугольника. Если треугольник остроугольный, радиус центральной окружности будет находиться внутри треугольника. В случае, когда треугольник является прямоугольным, радиус будет проходить через середину гипотенузы. И, наконец, если треугольник тупоугольный, радиус окружности будет располагаться снаружи треугольника.
| Свойство | Радиус центральной окружности |
|---|---|
| Перпендикулярность | Пересекает стороны треугольника перпендикулярно |
| Отношение радиусов | Равен половине радиуса описанной окружности |
| Ориентация треугольника | Внутри, на гипотенузе или снаружи треугольника в зависимости от типа |
Вопрос-ответ

Как определить радиус вписанной окружности в треугольнике?
Для определения радиуса вписанной окружности в треугольнике можно воспользоваться формулой: радиус равен отношению площади треугольника к полупериметру треугольника. Или же можно воспользоваться формулой радиуса, основанной на длинах сторон треугольника.
Зачем нужно знать радиус вписанной окружности в треугольнике?
Знание радиуса вписанной окружности в треугольнике может быть полезным при решении геометрических задач и нахождении других характеристик треугольника, таких как площадь, стороны и углы. Также радиус вписанной окружности связан с центром вписанной окружности и может помочь определить его координаты.
Какова связь между радиусом вписанной окружности и углами треугольника?
Существует формула, связывающая радиус вписанной окружности и углы треугольника. Согласно этой формуле, радиус равен отношению площади треугольника к произведению полупериметра треугольника и тангенса половины каждого из его углов.
Влияет ли изменение размеров сторон треугольника на радиус вписанной окружности?
Да, изменение размеров сторон треугольника влияет на радиус вписанной окружности. Чем больше стороны треугольника, тем меньше радиус вписанной окружности, и наоборот. Это связано с тем, что площадь треугольника остается неизменной, но полупериметр треугольника увеличивается при увеличении его сторон.
Можно ли найти радиус вписанной окружности, зная только углы треугольника?
Да, можно найти радиус вписанной окружности, зная только углы треугольника. Для этого можно воспользоваться формулой радиуса вписанной окружности, которая основана на длинах сторон треугольника и тригонометрии. Также можно воспользоваться формулой, связывающей радиус и углы треугольника.
Зачем нужна вписанная окружность в треугольнике?
Вписанная окружность играет важную роль в геометрии треугольников. Она касается каждой стороны треугольника и имеет центр в его внутренней области. С помощью радиуса вписанной окружности можно вычислить площадь треугольника, его периметр, а также определить длины высот треугольника. Кроме того, свойства вписанных окружностей используются при решении различных геометрических задач.



