Часто приходится сталкиваться с задачами, требующими знания геометрии. В одной из таких задач необходимо найти координаты центра окружности при известном значении ее диаметра. Этот параметр имеет важное значение при построении графиков, создании точек в пространстве или при решении задач, связанных с расчетом площадей и длин. В данном разделе мы рассмотрим подходы к определению центра окружности с использованием доступных инструментов геометрии.
Первый метод, который мы рассмотрим, основан на использовании теоремы о прямоугольном треугольнике. Мы представим окружность как окружность, образованную диаметром, и разделим его на две равные части. Затем мы найдем ортогональные отрезки на каждой из половин диаметра, соединяющие концы диаметра с противоположными точками окружности. Затем мы найдем точку пересечения этих двух отрезков и определим ее как центр окружности. Этот метод основан на математических принципах нахождения пересечения прямых и может применяться в различных задачах геометрии.
Другой подход к определению центра окружности с использованием известного диаметра состоит в использовании геометрических принципов. В этом случае мы рассмотрим окружность с известным диаметром и построим непрерывную кривую, имеющую равные расстояния от каждой точки окружности до центра. Эта кривая называется окружностью. Далее мы найдем две точки на окружности, которые находятся на расстоянии, равном половине диаметра окружности. Затем мы построим отрезки, соединяющие эти две точки с концами диаметра, и найдем точку пересечения этих отрезков. Таким образом, мы можем определить центр окружности при известном диаметре.
Основные сведения и понятия для нахождения середины окружности
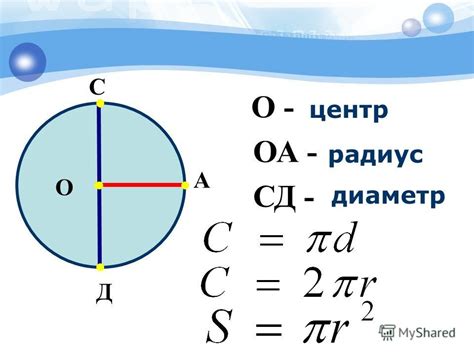
Диаметр - это отрезок, соединяющий любые две точки на окружности и проходящий через ее центр. Он является самым длинным отрезком в окружности и имеет особое значение при определении центра.
Радиус - половина диаметра окружности. Он также проходит через центр и помогает определить его положение.
Окружность - это геометрическая фигура, которая состоит из всех точек, равноудаленных от центра. Центр окружности является ключевым понятием, и его определение позволяет нам полностью описать окружность и ее свойства.
Середина - это точка, которая разделяет отрезок на равные части. В случае окружности, которая является симметричной, середина диаметра автоматически становится центром окружности.
Понимание этих понятий и описанных терминов является ключевым для определения положения центра окружности по известному диаметру. Чтобы найти центр окружности, следует использовать математические методы и определения, основанные на геометрических принципах.
Значение и важность геометрического понятия центра круга в контексте его функциональности

Центр круга - это точка, расположенная в его середине, от которой равноудалены все точки окружности. Данное понятие является фундаментальным и имеет большое значение в математике, архитектуре, строительстве, физике и других областях науки.
Центр круга отличается от других его компонентов и дает структуру окружности. Он служит отправной точкой для определения других важных параметров круга, таких как радиус, длина окружности, площадь и прилегающие линии.
Знание и понимание понятия центра круга является необходимым, чтобы эффективно работать с окружностями, прогнозировать и анализировать их свойства, использовать в практических задачах, например, в строительстве или проектировании. Также, понимание центра круга помогает в понимании и описании пространства и формы в геометрии, что имеет широкое применение в различных областях деятельности.
Размеры круга: выявление и измерение
- Методы измерения диаметра
- Точные инструменты для определения диаметра
- Альтернативные подходы к измерению диаметра
- Техники измерения в сложных условиях
Зависимо от доступных инструментов и окружающих условий, возможны различные методы измерения диаметра круга. Некоторые из них требуют использования точных инструментов, таких как штангенциркуль или микрометр, в то время как другие альтернативные подходы могут включать использование обычного линейного мерного инструмента, например, линейки или мерной ленты.
Также, в некоторых случаях, измерение диаметра может быть затруднено из-за особых условий, например, наличия выпуклых или вогнутых элементов на поверхности круга. В таких ситуациях могут применяться специальные техники измерения, такие как использование контуров или центрования объекта в специальном держателе.
Методы анализа для расчета координат середины окружности

Рассмотрение индикаторных точек и теорем о центре позволят нам вычислить положение точки пересечения диаметра с окружностью, а также определить середину диаметра. Другой метод включает в себя анализ системы уравнений, основанных на длине диаметра и относительных координатах на окружности. Это позволит нам найти точное положение центра окружности с использованием алгебраических операций.
| Метод | Описание |
|---|---|
| Метод геометрической конструкции | Определение координаты центра окружности с использованием принципов геометрии |
| Метод системы уравнений | Решение системы уравнений, основанных на длине диаметра и относительных координатах |
Эти методы могут быть полезны при моделировании и анализе окружностей в различных областях, таких как геометрия, физика, инженерия и компьютерная графика. Изучение деталей этих методов позволит получить глубокое понимание процесса определения центра круга и применить его в практических задачах.
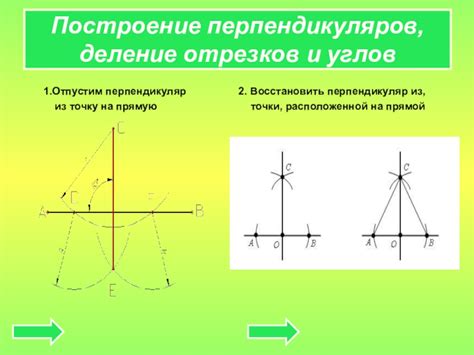
Метод построения перпендикуляра к диаметру
- Поставьте компас на конец диаметра круга. Это является отправной точкой, от которой мы будем строить перпендикуляр.
- Регулируя расстояние на компасе, нарисуйте дугу, которая пересекает диаметр в двух точках. Эти две точки будут служить как отправные точки для построения перпендикуляра.
- Возьмите другой конец диаметра и поставьте компас на него.
- Снова регулируя расстояние на компасе, нарисуйте дугу, которая пересекает диаметр в двух других точках. Эти две точки также будут служить как отправные точки для построения перпендикуляра.
- Используя линейку, соедините первую и вторую точки пересечения дуг с диаметром.
- Используя линейку, соедините третью и четвертую точки пересечения дуг с диаметром.
- Линия, которая пересекает диаметр и образует прямой угол с ним, будет перпендикуляром к диаметру.
Таким образом, данный метод позволяет нам легко и точно построить перпендикуляр к известному диаметру. Этот инструмент может быть использован в различных практических задачах, включая построение геометрических фигур, нахождение точек пересечения и решение геометрических задач.
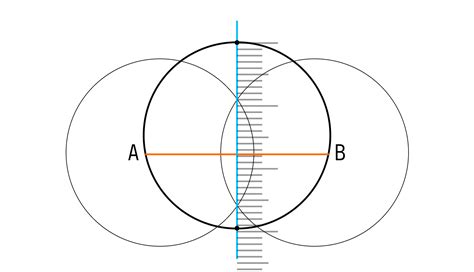
Метод построения хорд и их перпендикуляров
В данном разделе рассмотрим методику построения хорд и перпендикуляров к ним в контексте известного диаметра окружности. С помощью этих инструментов можно определить не только расположение хорды, но и ее длину и углы, которые она образует.
Хорда - это отрезок, который соединяет две точки на окружности. Она имеет свою определенную длину и расположение относительно центра окружности. Особый интерес представляют перпендикуляры к хорде - линии, которые пересекают хорду под прямыми углами. Эти перпендикуляры имеют особое значение при решении различных геометрических задач.
- Для построения хорды необходимо взять циркуль и установить его радиусом, равным половине диаметра окружности. Затем с помощью циркуля сделать две отметки на окружности, которые будут обозначать концы хорды.
- Чтобы построить перпендикуляр к хорде, нужно провести его из середины хорды. Для этого снова используем циркуль и сделаем радиус, равный половине длины хорды. С помощью циркуля проведем дугу от середины хорды, которая пересечет хорду на двух точках. Затем проведем линию, проходящую через эти точки - она будет перпендикуляром к хорде.
Таким образом, метод построения хорд и их перпендикуляров с использованием известного диаметра позволяет определить не только положение хорды, но и ее длину и углы. Этот метод является важным инструментом в геометрии и может быть использован при решении различных проблемных задач.
Метод разделения диаметра пополам

Суть этого метода заключается в следующем: необходимо провести две перпендикулярные линии через диаметр круга таким образом, чтобы они пересекались в произвольной точке на поверхности круга. Затем, используя эту точку пересечения, провести еще две перпендикулярные линии через другие две точки на диаметре круга. При правильной проведении этих линий, точка их пересечения будет являться центром круга.
Для наглядности и лучшего понимания данного метода, проиллюстрируем его на примере. Рассмотрим круг с известным диаметром. На его диаметре выберем две произвольные точки и проведем через них две перпендикулярные линии. После этого выберем еще две произвольные точки на диаметре, отличные от предыдущих двух, и проведем через них еще две перпендикулярные линии. Точка пересечения последних двух линий и будет являться центром круга.
| Шаг 1: | Выберем две произвольные точки на диаметре круга и проведем через них перпендикулярные линии. |
| Шаг 2: | Выберем еще две произвольные точки на диаметре, отличные от предыдущих двух, и проведем через них еще две перпендикулярные линии. |
| Шаг 3: | Точка пересечения последних двух линий является центром круга. |
Таким образом, применение метода разделения диаметра пополам позволяет определить центр круга с высокой точностью и без необходимости использования сложных вычислений или специального оборудования. Этот метод может быть полезен как в научных исследованиях, так и в повседневной жизни для определения центра круга в различных задачах, связанных с геометрией и конструкцией.
Геометрические приемы для определения центра окружности
В этом разделе мы рассмотрим различные геометрические методы, которые помогут нам определить точное положение центра окружности, исходя из известного диаметра. Наша задача состоит в том, чтобы найти точку внутри окружности, которая будет являться центром и с помощью которой мы сможем провести всех радиусы.
Один из наиболее распространенных способов определения центра окружности - это использование перпендикуляров. Мы можем провести перпендикуляр к диаметру в любой его точке, затем повторить эту операцию в другой точке диаметра. Точкой пересечения этих двух перпендикуляров будет центр окружности.
Еще один способ определить центр окружности - это провести диагональ к диаметру. Затем, используя эти две диагонали, мы можем провести две окружности с одним общим радиусом и найти точку пересечения этих окружностей. Эта точка будет являться центром окружности.
Также, мы можем воспользоваться секущими, чтобы определить центр окружности. Проведем две секущие к диаметру в разных точках. Затем проведем биссектрисы углов, образованных этими секущими. Точка пересечения биссектрис будет центром окружности.
Используя эти геометрические методы, мы можем определить центр окружности с высокой точностью, исходя из известного диаметра. Комбинируя различные методы, можно получить более надежные результаты и заранее избежать ошибок при проектировании и измерениях.
Использование инструментов для определения точного центра круга

В этом разделе мы рассмотрим методику нахождения точного центра круга с использованием инструментов, таких как циркуль и линейка. Эти орудия точности позволяют определить центр круга без использования сложной техники или вычислений.
Основная идея метода заключается в использовании геометрических принципов и инструментов для определения точки, являющейся центром круга. Для этого необходимо выполнить ряд простых шагов, используя циркуль и линейку в комбинации с геометрическими конструкциями.
Шаг 1: Закрепите циркуль на одной из точек окружности так, чтобы расстояние между центром циркуля и выбранной точкой окружности было таким же, как и радиус круга.
Шаг 2: Отметьте эту точку на бумаге и повторите шаг 1 для другой точки окружности. Используя линейку, проведите линию между двумя отмеченными точками.
Шаг 3: Повторите шаги 1 и 2 для двух других точек на окружности. Проведите линию, соединяющую эти точки.
Шаг 4: Точка пересечения всех проведенных линий является центром круга. Отметьте эту точку на бумаге.
Важно помнить, что для достижения наилучшей точности рекомендуется провести не менее трех таких линий, используя разные пары точек окружности. Точка пересечения всех линий даст наиболее точный результат для центра круга.
Построение равномерных выпуклых многоугольников вокруг окружности
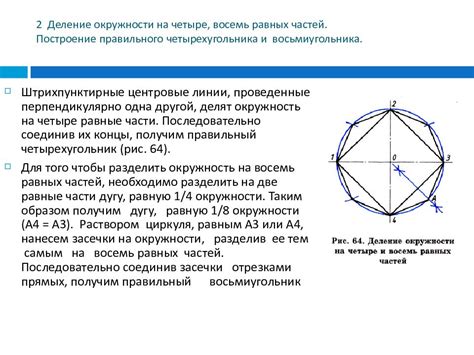
В данном разделе рассмотрим метод построения равномерных выпуклых многоугольников, которые описывают окружность. Эти многоугольники представляют собой особые фигуры, которые могут быть использованы в различных областях, таких как геометрия, дизайн и компьютерная графика.
Для построения равномерного выпуклого многоугольника вокруг окружности необходимо определить координаты его вершин. Один из способов получения этих координат заключается в использовании тригонометрических функций. Для этого можно разделить полный круг на равные углы и вычислить координаты вершин с помощью формул синуса и косинуса.
| Угол (в радианах) | Координата x | Координата y |
|---|---|---|
| 0 | x₀ = r | y₀ = 0 |
| π/4 | x₁ = r*cos(π/4) | y₁ = r*sin(π/4) |
| π/2 | x₂ = 0 | y₂ = r |
| 3π/4 | x₃ = r*cos(3π/4) | y₃ = r*sin(3π/4) |
| π | x₄ = -r | y₄ = 0 |
| 5π/4 | x₅ = r*cos(5π/4) | y₅ = r*sin(5π/4) |
| 3π/2 | x₆ = 0 | y₆ = -r |
| 7π/4 | x₇ = r*cos(7π/4) | y₇ = r*sin(7π/4) |
Повторяя этот процесс для каждого угла на интервале от 0 до 2π, можно получить координаты вершин выпуклого многоугольника. Равномерные выпуклые многоугольники, построенные вокруг окружности, характеризуются особым равномерным распределением вершин, которое обеспечивает симметрию и эстетичность.
Реальные примеры определения середины окружности
Этот раздел предлагает ознакомиться с практическими ситуациями, в которых необходимо определить центр окружности. Рассмотрим случаи нахождения середины окружности в различных сферах деятельности, где этот навык может пригодиться.
- Пример 1: Геометрия - изучение форм и фигур
- Пример 2: Инженерия - проектирование и строительство
- Пример 3: Медицина - лечение и диагностика
- Пример 4: Графический дизайн - создание иллюстраций
Математика и геометрия тесно связаны с определением центра окружности. Геометрические задачи требуют нахождения середины окружности, например, при построении окружности с заданным диаметром. Точное вычисление позволяет достичь точности в конструкции и измерениях.
В инженерии часто возникает потребность в определении середины окружности для точного размещения объектов и сооружений. Например, в строительстве зданий и мостов, определение центра основания позволяет строить конструкции с равномерным распределением нагрузок и стабильностью.
В медицине нахождение центра окружности может быть полезным для проведения операций и процедур, а также для диагностики и мониторинга заболеваний. Например, определение центра окружности позволяет точно локализовать опухоль или очертания органа при проведении лапароскопии и других хирургических вмешательствах.
В графическом дизайне определение середины окружности имеет значение для создания симметричных и пропорциональных изображений. Этот навык особенно полезен при создании логотипов, эмблем и иллюстраций, где точность и баланс являются важными аспектами.
Решение задачи на определение центра окружности по геометрическим данным

При работе с геометрическими задачами, возникающими в области аналитической геометрии, встречается такая задача: необходимо определить положение центра окружности, зная диаметр и некоторые другие геометрические данные.
Для решения данной задачи необходимо учесть ряд факторов и использовать определенные математические методы.
Рассмотрим подходящий способ решения задачи на определение координат центра окружности, при известном диаметре окружности и координатах двух произвольных точек на данной окружности.
- Шаг 1: Выберите две произвольные точки на окружности и определите их координаты.
- Шаг 2: Рассчитайте середину отрезка, соединяющего эти две точки.
- Шаг 3: Получите координаты центра окружности, учитывая, что центр окружности находится на перпендикуляре, проходящем через середину отрезка, соединяющего две заданные точки, и расстояние от центра до каждой из этих точек равно половине диаметра окружности.
Таким образом, при наличии известного диаметра окружности и координат двух точек на окружности, можно определить координаты центра окружности, используя рассмотренный выше метод.
Вопрос-ответ

Как определить центр круга при известном диаметре?
Для определения центра круга при известном диаметре необходимо провести два любых перпендикулярных диаметра, соединить их концы и найти точку пересечения. Эта точка будет являться центром круга.



