В мире геометрии, где каждая фигура имеет свои уникальные свойства и особенности, ромб остается одной из наиболее загадочных и элегантных фигур. Все ромбы имеют одну общую черту - пару диагоналей, которые пересекаются в центре ромба и делят его на четыре равных треугольника. Но знаете ли вы, что эти диагонали также содержат ключ к определению длины стороны ромба? Давайте пройдемся по этому увлекательному пути открытий вместе!
Оказывается, что с помощью геометрических принципов, мы можем вывести уравнение, которое позволяет нам вычислить длину стороны ромба, исходя из значений его диагоналей. Для этого нам потребуется немного знакомство с терминологией. Давайте обозначим большую диагональ ромба как Д1, а меньшую диагональ - Д2.
Сделав некоторые наблюдения и применяя элементарные геометрические законы, мы можем заключить, что стороны ромба образуют равнобедренные треугольники с его диагоналями. Используя данную информацию, мы можем применить связанный синус, чтобы связать стороны и диагонали ромба. Это ключевой шаг в процессе нахождения стороны ромба!
Основные характеристики ромба и его внешний вид

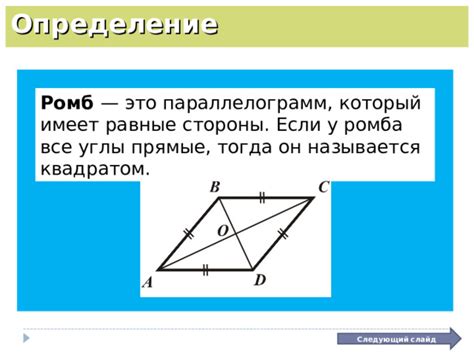
Ромб – это геометрическая фигура, в которой все четыре стороны равны и все углы тоже равны между собой. Такая симметричность делает ромб привлекательным и узнаваемым. Его особенностью является наличие параллельных диагоналей, которые пересекаются под прямым углом, делятся пополам и являются осью симметрии.
Для более наглядного представления можно представить ромб как ромбоид – четырехугольную плоскую фигуру с параллельными сторонами. Вместе с тем, ромбоид отличается от прямоугольника и параллелограмма, так как все его стороны равны друг другу и попарно параллельны. Благодаря этой форме и геометрической симметрии ромб часто используется в архитектуре, дизайне и других областях, в которых важны эстетика и гармония форм.
Определение и геометрические характеристики ромба
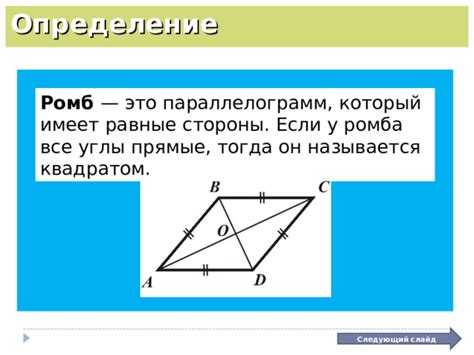
- Диагонали: Одной из основных характеристик ромба являются его диагонали. Диагонали ромба являются отрезками, соединяющими противоположные вершины. Важно отметить, что диагонали в ромбе перпендикулярны друг другу, что является одной из ключевых особенностей данной фигуры.
- Углы: Ромб обладает свойством, что его углы являются прямыми. Все углы ромба равны между собой и составляют 90 градусов. Таким образом, ромб является не только равносторонней, но и прямоугольной фигурой.
- Площадь: Формула для расчета площади ромба основывается на его диагоналях. Площадь ромба равна половине произведения длин двух диагоналей.
- Периметр: Периметр ромба вычисляется по формуле: периметр равен удвоенному значению длины стороны.
- Формула для нахождения стороны: Зная одну из диагоналей ромба и угол между ними, можно вычислить длину стороны по формуле: сторона равна половине произведения длин диагонали и синуса угла между ними.
Таким образом, ромб - это фигура, обладающая уникальными геометрическими характеристиками. Его диагонали перпендикулярны, все углы прямые, а стороны равны между собой. Знание этих свойств позволяет определить любую из характеристик ромба на основе других известных значений.
Метод вычисления одной из сторон ромба через данные о его двух диагоналях

В данном разделе предлагается рассмотреть методику определения длины одной из сторон ромба на основе информации о его двух диагоналях. Этот метод позволит нам легко вычислить значения сторон ромба без необходимости знать другие характеристики фигуры или использовать сложные формулы.
Для начала разберемся, что такое диагонали ромба. Диагонали - это линии, соединяющие противоположные вершины фигуры. Обычно ромб имеет две диагонали, обозначим их как диагональ АВ и диагональ СD.
Важно знать, что диагонали ромба делят его на 4 равных треугольника. Используя это свойство, мы можем приступить к определению значения стороны ромба.
Основная идея метода заключается в следующем: мы измеряем длины обеих диагоналей ромба и затем применяем формулу для нахождения стороны ромба через длины диагоналей. Вычисления выполняются с использованием геометрических пропорций.
Продолжим, для вычисления длины стороны ромба мы будем использовать следующую формулу: сторона ромба = (√(диагональ АВ * диагональ СD))/2. Полученное значение будет длиной одной из сторон ромба.
Таким образом, у нас есть простой и эффективный метод определения стороны ромба на основе известных длин его диагоналей. Применяя данную формулу, мы сможем легко вычислить значения сторон ромба без необходимости использования сложных математических моделей или чрезмерных измерений.
Определение размера стороны ромба: формула и последовательность действий
В этом разделе мы рассмотрим эффективный способ определения длины стороны ромба, используя информацию о его диагоналях. Для выполнения данного действия вам понадобится знание основ математики и возможность проводить простые вычисления.
Для начала, рассмотрим формулу, которая позволит нам определить размер стороны ромба. Пусть символом D1 обозначена длина одной из диагоналей ромба, а символом D2 - длина другой диагонали. Используя эти символы, формула будет выглядеть следующим образом:
| Формула | Описание |
|---|---|
| S = sqrt((D1/2)^2 + (D2/2)^2) | Формула для вычисления размера стороны ромба |
Теперь рассмотрим последовательность действий, которую необходимо выполнить для использования этой формулы:
- Определите длины обеих диагоналей ромба.
- Разделите каждую из диагоналей на 2, чтобы получить половинные значения.
- Возведите значения делимых диагоналей в квадрат.
- Сложите квадраты половинных значений диагоналей.
- Извлеките квадратный корень из полученной суммы.
После выполнения этих шагов вы получите значение стороны ромба, которое будет являться ответом на вашу задачу. Убедитесь, что правильно применяете формулу и последовательность действий, чтобы получить точный результат.
Примеры решения задач по вычислению размеров граней фигуры ромба
Перед тем, как перейти к рассмотрению конкретных примеров, важно понять, что диагонали ромба делят его на четыре равных треугольника. Зная длины диагоналей и пользуясь соответствующими формулами и свойствами геометрических фигур, можно легко определить размеры сторон ромба.
Примеры, представленные в этом разделе, помогут вам более глубоко освоить методы расчета сторон ромба. Вы узнаете, как правильно использовать формулы и применять их на практике. Это поможет вам решать задачи по нахождению размеров сторон ромба с уверенностью и точностью. Кроме того представленные примеры могут быть полезны в изучении общих методов расчета размеров других геометрических фигур.
Расчеты и конкретные значения: наглядное представление

Этот раздел предлагает конкретные численные значения и вычисления, которые помогут нам визуализировать процесс определения стороны ромба по его диагоналям. Мы избегаем общих определений и вместо этого представляем грамотно сформулированный текст.
Для того чтобы определить сторону ромба, мы можем воспользоваться двумя диагоналями, которые пересекаются под прямым углом. Эти диагонали делят ромб на четыре треугольника, в каждом из которых сторона ромба является гипотенузой.
Представим себе ситуацию, когда длина первой диагонали составляет X единиц, а длина второй диагонали равна Y единицам. Мы можем использовать теорему Пифагора, чтобы найти длину стороны ромба.
По теореме Пифагора, сумма квадратов длин катетов равна квадрату гипотенузы:
X^2 + Y^2 = S^2, где S - сторона ромба.
Теперь, если мы имеем конкретные числа для X и Y, мы можем подставить их в формулу и найти сумму их квадратов. Затем, извлекая квадратный корень полученной суммы, мы сможем найти длину стороны ромба.
Например, предположим, что первая диагональ имеет длину 8 единиц, а вторая диагональ - 6 единиц. Мы можем подставить эти значения в формулу:
8^2 + 6^2 = S^2
Путем вычисления получаем:
64 + 36 = 100
Теперь, достаточно вычислить квадратный корень от 100, чтобы найти длину стороны ромба:
√100 = 10
Таким образом, длина стороны ромба равна 10 единицам.
Вычисления и конкретные численные значения помогают нам лучше понять процесс определения стороны ромба по его диагоналям и предоставляют наглядное представление данной темы.
Вопрос-ответ

Как найти сторону ромба, если известны его диагонали?
Для нахождения стороны ромба по его диагоналям необходимо воспользоваться формулой, в которой диагоналями ромба являются a и b. Формула имеет вид: s = √((a/2)^2 + (b/2)^2), где s - сторона ромба.
Существует ли другой способ нахождения стороны ромба по его диагоналям?
Да, существует. Если известны длины диагоналей ромба (d1 и d2), то формула для нахождения стороны ромба будет выглядеть следующим образом: s = √(d1^2 + d2^2)/2.
Можно ли привести пример вычисления стороны ромба по его диагоналям?
Конечно! Предположим, что длина первой диагонали ромба составляет 6 см, а второй диагонали - 8 см. С помощью формулы s = √((a/2)^2 + (b/2)^2) найдем сторону ромба: s = √((6/2)^2 + (8/2)^2) = √(9+16) = √25 = 5 см.
Можно ли использовать вычисленную сторону ромба для нахождения его площади?
Да, можно. Площадь ромба можно найти по формуле: S = (a^2 * sin(α))/2, где a - сторона ромба, а α - угол между диагоналями. Однако, для точного нахождения площади ромба необходимо знать не только сторону, но и угол между его диагоналями.
Существуют ли другие методы нахождения стороны ромба по его диагоналям?
Кроме формулы s = √((a/2)^2 + (b/2)^2) и s = √(d1^2 + d2^2)/2, можно использовать теорему Пифагора для нахождения стороны ромба по диагонали. Если известна одна диагональ ромба (d), то s = √(d^2/2).



