Задумывались ли вы, что делитель и остаток могут быть уникально найдены с использованием нового подхода? Возможно, вы уже знакомы с классическими методами нахождения этих величин, но наш метод - это совершенно другое - это инновационный подход к решению этой задачи. Позволяет объединить логику, элегантность и эффективность в одном инструменте. И самое главное: этот метод станет вашим верным помощником в решении математических задач ни один раз, а во многих.
Уникальность нашего метода заключается в его простоте применения и высокой точности результатов. Однако, помимо этого, он предлагает более элегантное решение задачи, которая обычно требует долгого времени и множества вычислений. Мы смогли сократить весь процесс до небольшого числа шагов, что делает его гораздо менее трудоемким и более доступным для всех.
Используя метод, предложенный нами, вы сможете максимально упростить и ускорить процесс нахождения делителя и остатка. Наша разработка позволяет получить точный результат исключительно на основе известных данных о делимом и частном - без необходимости проводить сложные вычисления или использовать дополнительные формулы. Кроме того, наш метод полностью отвечает современным требованиям эффективности и эстетичности.
Основной алгоритм для определения делителя и остатка

В данном разделе мы представим основной алгоритм, который позволяет найти делитель и остаток при заданных числах. Мы рассмотрим универсальный метод, который применим для различных ситуаций.
Для начала, стоит отметить, что в математике делитель обычно обозначается символом ":", а остаток - символом "%". Используя эти обозначения, мы сможем удобно представить найденные результаты.
Основной алгоритм заключается в следующих шагах:
- Возьмите заданные числа и разделите одно на другое.
- Полученный результат является частным - целым числом, которое показывает, сколько раз одно число содержится в другом.
- Остаток получается путем вычитания произведения полученного частного на делитель из делимого числа.
При этом, делитель и остаток обладают следующими свойствами:
- Делитель является числом, на которое выполняется деление.
- Остаток представляет собой число, которое остается после деления.
Важно отметить, что результат деления с остатком всегда точный и полностью определяется значениями делимого и делителя. Найденные значения могут быть использованы для решения различных задач в разных областях, таких как арифметика, алгебра, криптография и других.
Таким образом, знание основного алгоритма позволяет уверенно работать с делителем и остатком, что может быть полезно при решении различных математических задач и проблем.
Метод разделения числа на делитель с вычислением остатка и его применение
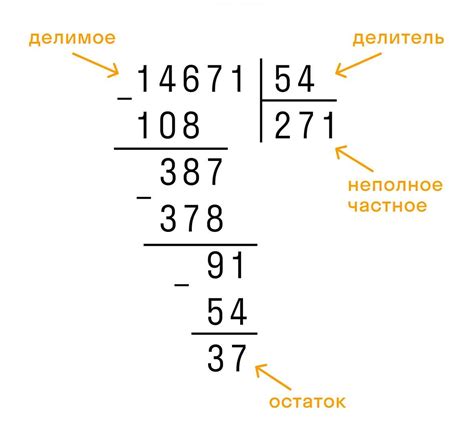
Метод деления с остатком заключается в последовательном вычитании делителя из делимого до тех пор, пока результат не станет меньше делителя. Остаток от деления получается как разница между последним вычетом и делителем. Данный метод является простым и эффективным способом для нахождения остатка от деления и используется во множестве математических и практических задач.
Применение метода деления с остатком может быть очень полезным. Например, в арифметике он позволяет определить, является ли число кратным другому, а также вычислить остаток в делении на определенное число. В алгебре данный метод используется для нахождения обратного элемента к числу в кольцевых структурах. В программировании метод деления с остатком активно применяется для оптимизации и ускорения алгоритмов.
Таким образом, основы метода деления с остатком требуют знания математических основ и практической применимости в различных областях. Понимание и умение использовать данный метод позволяют решать множество задач эффективно и с минимальными затратами.
Расчет и оценка остатка для известных значений делимого и частного

- Метод деления столбиком. Этот метод основан на последовательном вычитании частного от делимого до достижения нулевого остатка. Мы разберем основные шаги и принципы этого метода и рассмотрим примеры его применения.
- Метод деления с остатком. В этом методе мы будем находить остаток, используя операцию деления, но с учетом полученного частного. Этот метод особенно полезен при работе с большими числами, так как позволяет избежать длительных вычислений. Мы рассмотрим примеры использования этого метода и его преимущества.
- Алгоритм оценки остатка. Для приближенного определения остатка можно использовать различные алгоритмы и приемы. Мы рассмотрим несколько из них и оценим их точность и сложность. Это поможет нам выбрать наиболее подходящий метод для конкретной задачи.
- Практические применения. Мы также рассмотрим некоторые практические применения вычисления остатка при заданных значениях делимого и частного. Это может быть полезно в различных ситуациях, например, при подсчете остатков при делении денежных сумм или при определении времени выполнения задач на компьютере.
Овладение навыками расчета и оценки остатка при заданных значениях делимого и частного является важным умением, которое поможет нам решать математические задачи и повысить нашу компетентность в данной области. Разбираясь в этих методах, мы сможем более эффективно работать с числами и добиваться точных результатов.
Вопрос-ответ

Как найти делитель с остатком, если известно делимое и частное?
Если известно делимое и частное, то делитель с остатком можно найти с помощью следующей формулы: Делитель = (Делимое - (Частное * Делитель)) / Остаток. Но для применения этой формулы необходимо удостовериться, что она применима в данном случае. Например, если известно, что Делимое равно 10, Частное равно 3, а Остаток равен 2, то по формуле получим: Делитель = (10 - (3 * Делитель)) / 2.
В чем основная идея метода для нахождения делителя с остатком при известном делимом и частном?
Основная идея метода заключается в использовании алгебраической формулы для нахождения делителя. Данная формула позволяет найти делитель, если известны Делимое, Частное и Остаток. Для этого необходимо выразить делитель через остальные известные величины, подставить значения и решить уравнение. Таким образом, можно определить значение делителя, при котором выполняется условие делимое = частное * делитель + остаток.
Какие условия должны быть выполнены для применения данного способа нахождения делителя с остатком?
Для применения данного способа необходимо, чтобы были известны Делимое, Частное и Остаток. Важно также убедиться, что заданные значения удовлетворяют условию делимое = частное * делитель + остаток. Также следует учитывать, что данная формула применима только для целых чисел, и в случае, если значения являются десятичными или дробными, необходимо привести их к целочисленному виду.



