Современный мир информационных технологий предлагает множество инструментов, с помощью которых можно анализировать и оценивать большие объемы данных. Один из самых популярных таких инструментов - программа, позволяющая работать с табличными данными. Одна из наиболее известных программ данного типа - эксель.
При работе с большим объемом данных часто возникает необходимость найти взаимосвязь между различными числовыми значениями. Это может быть полезно для анализа трендов, прогнозирования будущих значений или выявления факторов, влияющих на результаты исследования. В эксель есть инструменты, позволяющие находить и определять степень корреляции между различными наборами данных.
В данной статье мы рассмотрим несколько способов обнаружения и измерения взаимосвязи между данными в эксель. От простых методов, таких как графическое представление данных, до более сложных, включающих использование статистических функций и формул. Вам не понадобятся специфические знания или сложные алгоритмы, чтобы воспользоваться этими инструментами - все, что нужно, это аналитический склад ума и небольшое понимание работы с таблицами и данными в эксель.
Зачем нужна корреляция и что она означает?
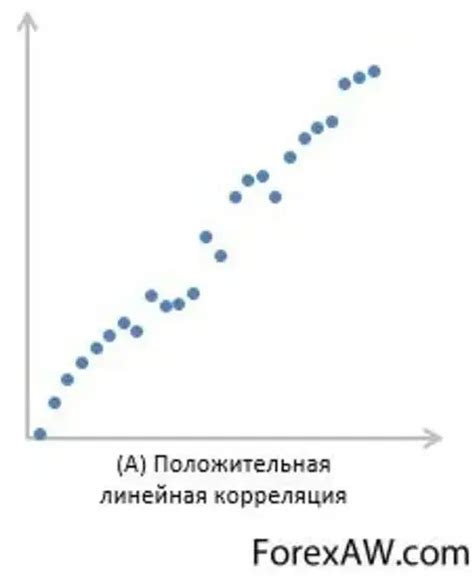
Высокая корреляция может указывать на прямую связь, когда две переменные меняются в одном направлении. Например, в случае с ростом температуры воздуха, количество продаж мороженого также может увеличиваться. Низкая корреляция, наоборот, может означать, что две переменные практически не связаны друг с другом.
Изучение корреляции может быть полезным при принятии решений в различных областях, таких как экономика, маркетинг, медицина и т.д. Например, зная корреляцию между потреблением фастфуда и уровнем сердечно-сосудистых заболеваний, можно предпринять меры для улучшения общественного здоровья. Таким образом, понимание корреляции и умение ее находить являются важными навыками в анализе данных и принятии обоснованных решений.
Важность умения анализировать взаимосвязи данных в программе для работы с электронными таблицами

Корреляция - один из основных инструментов статистического анализа данных, который позволяет изучать связь между различными переменными. Понимание и умение находить корреляцию в "Excel" является ценным навыком для людей, работающих с данными, так как позволяет выявлять взаимосвязи и определять их степень.
|
|
Вычисление корреляции: Основные шаги для анализа связи между переменными

Рассмотрим основные этапы для определения степени связи между различными переменными в данных и вычисления корреляции. Понимание таких связей может помочь нам лучше понять взаимосвязь между различными явлениями или факторами, что может привести к более глубоким исследованиям и принятию осознанных решений.
Одним из ключевых шагов при анализе корреляции является подготовка данных. Необходимо выбрать две переменные, которые предполагается связать между собой, и убедиться, что они представлены в числовом формате. Далее необходимо подготовить таблицу, в которой будут содержаться эти переменные.
| Переменная X | Переменная Y |
|---|---|
| Значение 1 | Значение 1 |
| Значение 2 | Значение 2 |
| Значение 3 | Значение 3 |
После подготовки данных необходимо проанализировать связь между переменными. Для этого часто используется корреляционный анализ, который позволяет определить, насколько сильная или слабая связь между переменными. В этом анализе часто применяется коэффициент корреляции, который демонстрирует направление и силу связи.
Коэффициент корреляции может принимать значения от -1 до 1. Значение 1 указывает на положительную линейную связь, а значение -1 - на отрицательную линейную связь. Значение близкое к 0 указывает на отсутствие связи между переменными.
Для вычисления коэффициента корреляции можно использовать различные методы, такие как формула Пирсона или ранговая корреляция Спирмена. Оба метода позволяют определить степень взаимосвязи между переменными, но выбор метода зависит от характера данных и целей исследования.
В целом, вычисление корреляции представляет собой важный инструмент для анализа связей между переменными. Основные шаги, описанные выше, помогут вам начать анализ данных и получить предварительное представление о взаимосвязях между переменными.
Выбор данных для проведения анализа
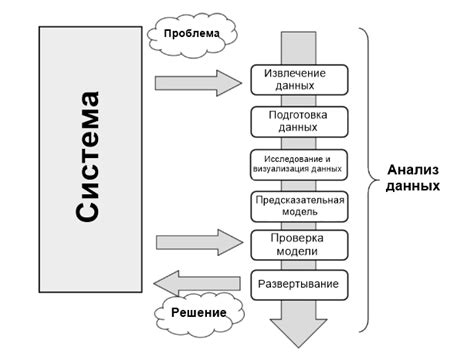
Первым шагом является определение цели исследования, чтобы понять, какие данные и переменные могут быть релевантными для достижения этой цели. Необходимо обратить внимание на специфику исследования и выделить факторы, аспекты или характеристики, которые могут влиять на явление, объект или процесс, который предмет анализа. Используйте синонимы слова "выбор" для описания данной части процесса.
Далее следует произвести первоначальную оценку доступных данных. Это включает в себя анализ исходных данных для определения их полноты, достоверности и актуальности. Затем проведите предварительный анализ данных, для выявления каких-либо выбросов, неточностей или пропущенных значений. Уделите внимание также вариативности данных и наличию достаточного объема данных для проведения корреляционного анализа. Используйте синонимы для выражения "первоначальная оценка" и "предварительный анализ".
Важным этапом является выбор конкретных переменных или показателей для проведения корреляционного анализа. Определите, какие переменные наиболее релевантны для вашего исследования и релевантны для изучаемой проблемы. Выберите переменные, которые наиболее полно отражают цель исследования и могут вносить значимый вклад в аналитический процесс. Используйте синонимы для слов "выбор переменных".
Примеры применения формул в Excel для расчета взаимосвязи данных
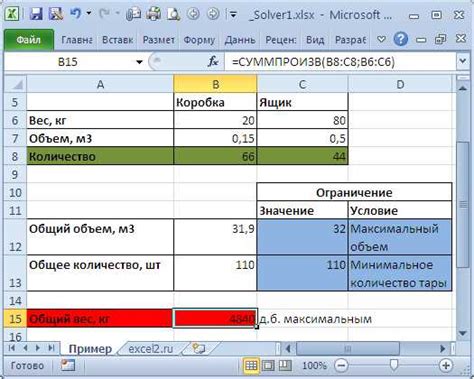
В данном разделе мы рассмотрим примеры использования формул в Excel, которые помогут подсчитать степень взаимосвязи между различными наборами данных. Отслеживание корреляции между данными позволяет нам увидеть, есть ли взаимная зависимость между двумя или более переменными, и насколько она сильна. Подобные расчеты имеют важное значение в таких областях, как финансы, экономика, социология и др.
Наши примеры включают использование различных формул для подсчета корреляции, таких как коэффициент Пирсона, коэффициент Спирмена и ковариация. Мы также рассмотрим случаи, когда степень взаимосвязи может быть положительной, отрицательной или даже отсутствовать.
- Пример 1: Расчет коэффициента Пирсона
- Пример 2: Расчет коэффициента Спирмена
- Пример 3: Расчет ковариации
- Пример 4: Сравнение результатов и интерпретация
В каждом примере мы пошагово рассмотрим процесс расчета корреляции и предоставим подробные инструкции и формулы, которые нужно использовать. Это поможет вам лучше понять, как применять эти формулы к вашим данным и получить точные результаты.
Использование формул в Excel для расчета корреляции дает возможность проводить качественный анализ данных и принимать обоснованные решения на основе полученных результатов. Отслеживание и изучение взаимосвязи между переменными поможет вам лучше понять и проанализировать данные, что очень полезно в различных сферах деятельности.
Анализ результатов корреляции: понимание взаимосвязей и их значимости

Корреляция - это статистическая мера, которая позволяет изучать связь между двумя или более переменными. Результаты корреляционного анализа могут указывать на то, насколько тесно связаны эти переменные и какова направленность этой связи. Однако, для правильного понимания результатов корреляции необходимо учитывать не только значимость статистической связи, но и направление связи, а также другие факторы, которые могут влиять на полученные значения.
- Определение направленности взаимосвязи: положительная или отрицательная корреляция. Положительная корреляция означает, что увеличение значения одной переменной соответствует увеличению значения другой переменной (например, чем больше время уделяется учебе, тем выше оценки). Отрицательная корреляция, в свою очередь, означает, что увеличение значения одной переменной соответствует уменьшению значения другой переменной (например, чем больше стресс, тем ниже уровень счастья).
- Значимость корреляции: определение статистической значимости связи между переменными. При интерпретации результатов корреляционного анализа важно учитывать p-значение, которое указывает на вероятность получить подобную взаимосвязь случайно. Чем меньше p-значение, тем более значимой является корреляция между переменными.
- Предельные значения коэффициента корреляции: понимание степени связи между переменными. Коэффициент корреляции, изменяющийся в диапазоне от -1 до +1, определяет силу и направление взаимосвязи. Значение коэффициента ближе к -1 или +1 указывает на более сильную взаимосвязь, в то время как значение ближе к 0 означает слабую или отсутствующую связь.
Вопрос-ответ

Как найти корреляцию в эксель?
Для нахождения корреляции в эксель необходимо использовать функцию "КОРРЕЛ". Для этого выберите два диапазона данных, между которыми хотите найти корреляцию, и введите формулу "=КОРРЕЛ(диапазон данных1; диапазон данных2)" в ячейку, где хотите получить результат. После этого нажмите Enter. Результатом будет значение корреляции, которое находится в диапазоне от -1 до 1.
Существуют ли альтернативные способы нахождения корреляции в эксель?
Да, в эксель также доступна функция "КОРРЕЛС", которая позволяет находить корреляцию для более чем двух диапазонов данных. Для этого выберите все необходимые диапазоны данных и введите формулу "=КОРРЕЛС(диапазон данных1; диапазон данных2; ...)" в ячейку, где хотите получить результат. Также существуют другие методы нахождения корреляции, например, с использованием диаграмм рассеяния и анализа регрессии.
Как интерпретировать результаты корреляции, полученные в эксель?
Значение корреляции, полученное в эксель, может находиться в диапазоне от -1 до 1. Значение близкое к -1 указывает на обратную корреляцию, то есть связь между двумя переменными, при которой одна увеличивается, а другая уменьшается. Значение близкое к 1 указывает на прямую корреляцию, то есть связь между двумя переменными, при которой обе увеличиваются или уменьшаются. Значение близкое к 0 указывает на отсутствие связи. Важно также учитывать статистическую значимость корреляции и проводить дополнительный анализ для получения более точных выводов.



