Искусство на этом свете простирается во множестве форм и выражений. Оно отражает глубину человеческой природы, открывая перед нами неизведанные горизонты творчества. Существует целый мир способов визуального представления идей, мыслей и объектов. Однако, несмотря на эту богатую разнообразность, некоторые геометрические фигуры сохраняют свое уникальное влечение для нас.
Одной из таких фигур является треугольник, величественное сочетание линий и углов, но есть и одно более стоящее сочетание этой фигуры – треугольник описанный около окружности. Этот треугольник обладает особым очарованием, которое сложно описать словами. Его форма, симметрия и совершенство восхищают нас и позволяют нам увидеть в нем гармонию самой природы.
Сегодня мы поговорим о том, как визуализировать эту элегантную фигуру. Мы расскажем о техниках и методах, при помощи которых можно нарисовать треугольник, охватывающий окружность. Мы познакомимся с инструментами, которые помогут нам справиться с этой задачей и погрузиться в мир геометрии и творчества одновременно.
Описание геометрической связи между треугольником и окружностью
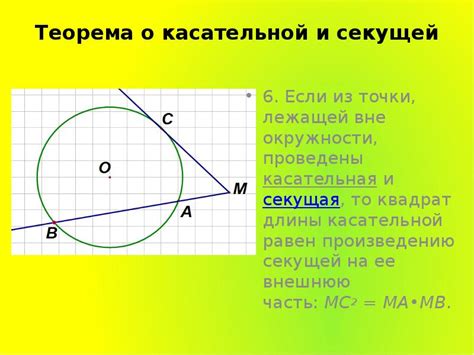
При вписывании треугольника в окружность, его вершины лежат на окружности, а стороны треугольника являются хордами окружности. Важно отметить, что для вписанного треугольника выполняются некоторые специфические свойства, которые проводят связи с радиусами и углами.
| Свойства вписанного треугольника | Описание |
|---|---|
| Сумма углов | Сумма углов вписанного треугольника всегда равна 180 градусов. |
| Углы, опирающиеся на одну и ту же дугу | Углы, опирающиеся на одну и ту же дугу окружности, равны. |
| Соотношения сторон | Пропорциональные соотношения сторон вписанного треугольника существуют между отрезками, которые соединяют вершины треугольника с центром окружности. |
Вписанный треугольник имеет много интересных свойств и возможностей для применения в геометрии. Знание этих свойств позволяет решать различные задачи и находить смежные значения и отношения между элементами треугольника и окружности.
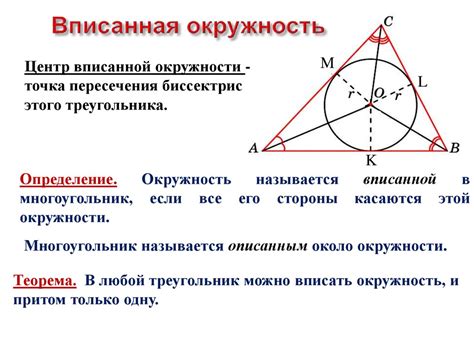
Построение центра внутренней окружности треугольника
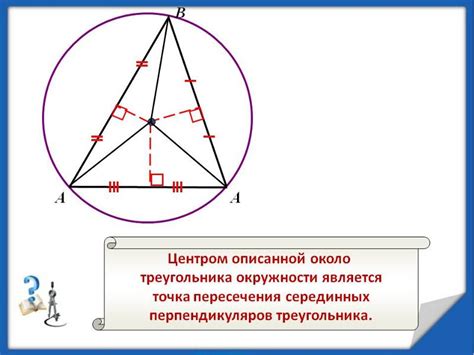
В данном разделе рассмотрим процесс построения центра окружности, которая вписана в заданный треугольник.
Для начала необходимо определиться с тем, что такое вписанная окружность. Это окружность, которая касается всех трех сторон треугольника. Особенность внутренней окружности заключается в том, что ее центр лежит внутри треугольника, а радиус равен расстоянию от центра до любой из сторон треугольника.
Для построения центра вписанной окружности треугольника можно использовать несколько методов. Один из самых известных методов основывается на возможности построить биссектрису каждого угла треугольника.
Построение биссектрисы угла треугольника производится путем деления угла пополам. Для построения биссектрисы с помощью геометрических инструментов можно использовать циркуль и линейку. Процесс построения биссектрисы требует точности и внимательного выполнения геометрических операций.
Затем, найдя все три биссектрисы, их пересечение будет являться центром вписанной окружности треугольника. С использованием центра окружности можно построить саму окружность, проведя радиус в любую точку на одной из сторон треугольника.
Таким образом, построение центра внутренней окружности треугольника позволяет определить ее положение относительно сторон треугольника и образует основу для построения и изучения различных свойств вписанной окружности.
Определение радиуса вписанной окружности
В этом разделе рассматривается метод определения радиуса вписанной окружности для треугольника, без использования прямых определений и визуальных представлений. Будут представлены альтернативные формулировки и синонимы, которые помогут лучше понять процесс нахождения радиуса вписанной окружности.
Исследование точек пересечения окружности и сторон треугольника

Для начала проведем подробный анализ с помощью таблицы, в которой будут представлены характеристики каждого случая пересечения окружности и сторон треугольника. Мы приведем значения углов и длин отрезков, а также указанное число точек пересечения для каждого сценария.
| Сценарий | Углы треугольника | Длины отрезков | Количество точек пересечения |
|---|---|---|---|
| Пересечение одной стороны треугольника | Угол 1, Угол 2, Угол 3 | Отрезок 1, Отрезок 2, Отрезок 3 | 1 |
| Пересечение двух сторон треугольника | Угол 1, Угол 2, Угол 3 | Отрезок 1, Отрезок 2, Отрезок 3 | 2 |
| Пересечение всех сторон треугольника | Угол 1, Угол 2, Угол 3 | Отрезок 1, Отрезок 2, Отрезок 3 | 3 |
В каждом сценарии будут представлены конкретные значения углов треугольника и длин отрезков, а также количество точек пересечения. Мы проведем детальное исследование каждого случая и дадим подробные пояснения о взаимном расположении окружности и сторон треугольника.
Исследование точек пересечения окружности и сторон треугольника является ключевым аспектом в геометрии и позволяет лучше понять связь между этими двумя геометрическими фигурами.
Построение вертикального отрезка и линии, равноугольной оси разделения треугольника, с применением внутренней окружности
Первая линия, которую мы рассмотрим, это высота треугольника. Она представляет собой вертикальный отрезок, проведенный из вершины треугольника, перпендикулярно к основанию, то есть к стороне треугольника. Высота является опорной линией и используется во многих геометрических расчетах треугольников.
Вторая линия, которую мы изучим, это биссектриса угла. Биссектриса - это линия, которая делит угол между двумя сторонами треугольника на две равные части. Биссектриса проходит через вершину угла и пересекает противоположную сторону. Она играет важную роль при нахождении центра вписанной окружности в треугольник.
Используя вписанную окружность, можно построить эти две линии с помощью геометрических методов. Благодаря полученным линиям мы сможем расширить наши знания о треугольниках и использовать их для решения различных задач в геометрии.
Построение описанной окружности вокруг треугольника
Практические примеры и упражнения для закрепления изученного материала

В данном разделе представлены практические примеры и упражнения, которые помогут закрепить и углубить основные концепции, связанные с построением треугольника, описанного около окружности.
Пройдите серию упражнений, которые направлены на развитие ваших навыков в описанной области. Они помогут вам лучше понять геометрические принципы и способы построения данного треугольника.
- Упражнение 1: Определение центра описанной окружности. Найдите центр описанной окружности для заданного треугольника и отметьте его на вашей рисунке.
- Упражнение 2: Построение окружности. Восстановите окружность, описанную вокруг заданного треугольника с использованием центра и радиуса.
- Упражнение 3: Построение треугольника. Постройте треугольник, описанный около заданной окружности с использованием найденных ранее данных. Укажите вершины треугольника.
- Упражнение 4: Свойства треугольника. Исследуйте свойства треугольника, описанного около окружности, и определите, какие углы и стороны являются равными или пропорциональными.
- Упражнение 5: Практическое применение. Решите практическую задачу, связанную с построением треугольника, описанного около окружности, например, в контексте архитектуры или инженерии.
Попробуйте выполнить данные упражнения по порядку, внимательно следуя инструкциям и проводя необходимые измерения. Это поможет вам стать более уверенными в построении треугольников, описанных около окружностей, и применении полученных знаний в реальных ситуациях.
Вопрос-ответ

Как нарисовать треугольник описанный около окружности?
Для начала, отметьте центр окружности на листе бумаги. Затем, используя циркуль или компас, нарисуйте окружность. Далее, возьмите ручку или карандаш и определите точки пересечения окружности и ее радиуса. Соедините эти точки линиями, и вы получите треугольник, описанный около окружности.
Как правильно отметить центр окружности?
Чтобы отметить центр окружности, возьмите лист бумаги и нарисуйте две перпендикулярные линии. Затем, с помощью рулетки или линейки, найдите и отметьте точку, где пересекаются эти линии. Это и будет центр окружности.
Как выбрать радиус окружности для построения треугольника?
Радиус окружности для построения треугольника можно выбрать любым удобным способом. Вы можете использовать цифры, чтобы задать конкретный радиус, или выбрать произвольное значение. Используйте линейку или рулетку, чтобы отмерить радиус на листе бумаги.
Как соединить точки пересечения окружности и ее радиуса линиями?
Для того чтобы соединить точки пересечения окружности и ее радиуса линиями, возьмите ручку или карандаш и протяните линию от центра окружности до каждой из точек пересечения. Убедитесь, что линии проходят через эти точки и расположены равномерно на обеих сторонах от центра окружности.
Можно ли нарисовать треугольник, описанный около окружности без циркуля или компаса?
Да, можно нарисовать треугольник, описанный около окружности и без циркуля или компаса. Для этого можно использовать метод геометрической конструирования, например, с помощью перпендикуляров и угловых инструментов. Однако, использование циркуля или компаса облегчает и ускоряет процесс построения.
Как нарисовать треугольник описанный около окружности?
Чтобы нарисовать треугольник описанный около окружности, нужно взять центр окружности и провести радиус до любой точки на окружности. Затем провести радиус к другим двум точкам на окружности. Эти три отрезка будут сторонами треугольника.
Какие свойства имеет треугольник, описанный около окружности?
Треугольник, описанный около окружности, имеет несколько свойств. Например, все три вершины этого треугольника лежат на окружности. Каждый угол этого треугольника является внешним к любому из невписанных в окружность треугольников, имеющих общую сторону с исходным треугольником. Еще одним свойством этого треугольника является равенство мер вписанных углов, образованных сторонами треугольника и хордами, соединяющими концы сторон с центром окружности.



