В мире чертежей и графического моделирования существует множество сложных и уникальных задач. Одна из них - создание эллипса в изометрии на чертеже. Это задание требует не только отличного знания основ геометрии, но и творческого подхода к решению проблемы.
Изометрическая проекция - это способ отображения трехмерных объектов на плоскости, который сохраняет их пропорции вдоль всех трех осей. Это позволяет создавать объемные изображения, придающие чертежу глубину и реалистичность.
Эллипс - это элегантная геометрическая фигура, которая характеризуется симметричностью и гармоничностью своих линий. Это одна из наиболее сложных геометрических форм, поскольку строится на основе точек, линий и радиусов.
Сочетание эллипса и изометрической проекции на чертеже дает нам уникальный вызов. Необходимость точного воссоздания формы и размеров эллипса на плоскости требует от нас применения математических принципов и технического мастерства.
Изометрическая проекция
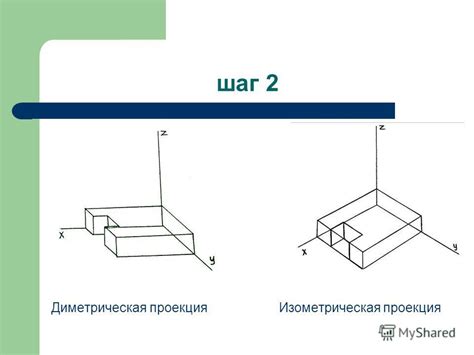
В данном разделе мы рассмотрим изометрическую проекцию, особый метод отображения трехмерных объектов на плоскости, который используется в чертежах. Изометрическая проекция позволяет создавать визуально достоверные изображения объектов, сохраняя их пропорции и формы.
Изометрическая проекция похожа на изображение, получаемое при наклонении предмета под углом и проекции на плоскость. Однако в отличие от ортогональной проекции, где обе оси пересекают плоскость под одинаковыми углами, в изометрической проекции одна ось пересекает плоскость под 30 градусами, а две другие под 60 градусами.
Этот угловой решёткичасто используется в судостроении и машиностроении, где точно отображение размеров и форм объектов является критическим. Изометрическая проекция также популярна в графическом и веб-дизайне, где она может быть использована для создания реалистичных и привлекательных визуальных композиций.
- Преимущества изометрической проекции:
- Сохраняет пропорции и формы объектов;
- Позволяет легко определить размеры объектов по осям;
- Предоставляет наглядное представление объекта в трех измерениях;
- Используется для создания реалистичных и привлекательных визуальных композиций.
Надеемся, что данный раздел поможет вам лучше понять и применять изометрическую проекцию в ваших проектах и чертежах.
Основные черты эллипса

В данном разделе мы рассмотрим основные характеристики и свойства эллипса, фигуры, которая обладает рядом особенностей и может быть описана с использованием различных параметров.
| Параметр | Описание |
| Большая и малая полуоси | Эллипс имеет две полуоси, главная из которых называется большой полуосью, а вторая - малой полуосью. Они определяют форму и размер эллипса. |
| Фокусы | Фокусы - это две точки, расположенные вдоль большой оси эллипса. Сумма расстояний от любой точки на эллипсе до фокусов всегда одинакова. |
| Эксцентриситет | Эксцентриситет характеризует степень "сплюснутости" фигуры эллипса и связан с отношением между большой и малой полуосями. |
| Периметр | Периметр эллипса представляет собой длину замкнутой кривой линии, образующей его границу. Расчет периметра зависит от значений полуосей. |
| Площадь | Площадь эллипса определяется его полуосями и представляет собой величину, равную площади плоской фигуры, заключенной внутри границ эллипса. |
Знание основных черт эллипса позволяет более полно представить и понять его характеристики, что может быть полезно при создании изометрических чертежей и других визуализаций.
Построение контура основной формы фигуры
- 1. Установите точки начала и конца главной оси эллипса, которые определяют его форму и размер.
- 2. Начиная с точки начала оси, установите несколько вспомогательных точек, определяющих сегменты фигуры.
- 3. Соедините вспомогательные точки поочередно, следуя непрерывно плавной кривой линии.
- 4. Постройте множество точек симметрично относительно главной оси, чтобы создать полный контур эллипса.
- 5. Убедитесь, что полученный контур соответствует заданным параметрам эллипса, таким как его основные размеры и форма.
Таким образом, построение основного контура эллипса - это определение начальных точек осей и последующее соединение сегментов фигуры в непрерывную кривую линию. Правильное выполнение этого этапа позволяет создать точную форму и соответствующие пропорции эллипса на чертеже.
Построение центральных осях эллипса

Раздел посвящен построению центральных осей эллипса, ключевых геометрических элементов, определяющих его форму и ориентацию в пространстве. В данном разделе будут представлены методы и алгоритмы, позволяющие определить положение и ориентацию центральных осей, а также их влияние на графическое представление эллипса.
Для построения центральных осей эллипса необходимо провести определенные геометрические действия, используя установленные геометрические законы и принципы. В процессе построения будут использоваться такие понятия, как эксцентриситет эллипса, его фокусные точки, а также оси симметрии и ось долготы.
Ось долготы является прямой, проходящей через центр эллипса и перпендикулярной центральным осям. Это важный элемент, определяющий направление эллипса в пространстве. Он служит ориентиром при построении и может быть использован для определения относительного положения других элементов на чертеже.
Оси симметрии проходят через центр эллипса и являются перпендикулярными друг другу. Они делят эллипс на две симметричные части и определяют его форму.
Понимание и умение строить центральные оси эллипса является важной компетенцией в области изометрического черчения и может быть полезным при создании точных и качественных чертежей.
Инструменты и техники для создания эллипсов

Для начала, необходимо выбрать подходящий инструмент для рисования эллипса. В зависимости от доступности и личных предпочтений, можно использовать как традиционные инструменты, так и цифровые программы. Традиционные инструменты включают циркуль, эллиптический шаблон или французский кривомерт. Если вы предпочитаете работать на компьютере, можно воспользоваться специализированными графическими программами, такими как Adobe Illustrator или AutoCAD.
Когда инструмент выбран, необходимо определить масштаб и ориентацию эллипса на чертеже. Масштаб определяется размером эллипса относительно других объектов на чертеже, а ориентация указывает на положение эллипса относительно осей координат.
Для построения эллипса с использованием циркуля, необходимо установить его радиус, центр и ориентацию. Если вы используете эллиптический шаблон или французский кривомерт, нужно приложить инструмент к чертежу и провести контур, используя указанные отметки и маркировки.
В случае работы с графическими программами, процесс создания эллипса может значительно отличаться. После выбора инструмента для создания эллипса, нужно указать его радиусы и центр на холсте или чертеже. В графических программах часто также доступны дополнительные опции для настройки внешнего вида и стиля эллипса.
В завершение процесса создания эллипса, необходимо проверить его точность и соответствие заданным параметрам. Оцените соотношение сторон эллипса, его симметрию и расположение относительно других объектов. Если нужно внести правки, воспользуйтесь соответствующим инструментом или функцией программы.
Итак, для успешного рисования эллипса на чертеже необходимо правильно выбрать инструмент, определить масштаб и ориентацию, выполнить построение согласно выбранному методу, а затем проверить результат на точность и соответствие заданным параметрам.
Вопрос-ответ

Как сделать эллипс в изометрии на чертеже?
Для того чтобы нарисовать эллипс в изометрии, необходимо использовать специальный метод. Сначала нарисуйте оси координат (длина осей должна быть одинакова). Затем выберите точку, которая будет являться центром эллипса. С помощью циркуля или другого инструмента, нарисуйте две длинные вертикальные линии, которые будут являться основными осями эллипса и проходят через переднюю точку центра. Затем проведите две короткие горизонтальные линии, которые будут соединять верхние и нижние концы вертикальных линий. Повторите эту операцию для задней точки центра, чтобы получить полный эллипс.
Существует ли специальный инструмент для рисования эллипсов в изометрии?
Наиболее распространенным инструментом для рисования эллипсов в изометрии является циркуль. Он позволяет более точно определить размеры и форму эллипса. Если циркуль отсутствует, можно использовать простую линейку и компас для рисования эллипса вручную. Однако это может потребовать больше времени и точности.
Какие применения имеет эллипс в изометрии на чертеже?
Эллипсы имеют множество применений в изометрическом чертеже. Они могут использоваться для изображения круглых предметов, таких как столбы, бочки или сосуды. Также они могут служить для создания эффекта глубины и трехмерности в изображении. Эллипсы также широко применяются в архитектурных чертежах для изображения окон, дверей и других деталей зданий.
Как изменить размеры эллипса в изометрии?
Для изменения размеров эллипса в изометрии необходимо изменить длину и положение его осей. Если необходимо увеличить или уменьшить размер эллипса, можно просто увеличить или уменьшить длину осей, сохраняя при этом их пропорциональное соотношение. Если требуется изменить форму эллипса, необходимо изменить положение осей.



