Волшебство математики всегда восхищало умы людей своей глубиной и точностью. Одним из ключевых понятий этой науки является НОД - наибольший общий делитель, который позволяет совершить слияние двух чисел в их общую суть. НОД неотъемлемо присутствует в каждом школьном курсе математики, и его поиск - настоящая находка для уверенного с изучением арифметики. Сегодня мы погрузимся в вселенную НОДа на страницах учебника Мерзляка и разберемся, каким образом совершить это открытие.
Проникнуться смыслом НОДа поможет нам пошаговое руководство и масса практических примеров. Ведь в математике, как и в реальной жизни, наиболее эффективным способом усвоения сложной информации является ее применение на практике. Благодаря такому подходу мы сможем в полной мере ощутить суть НОДа и его значение в математических рассуждениях.
Каждому школьнику непременно предстоит столкнуться с упражнениями, где нужно будет находить НОД. Это как особый критерий в проверяемом знании арифметики, который помогает доказать наши навыки и приумножить знания. Учебник Мерзляка, с его грамотно структурированным материалом и доступными объяснениями, станет настоящим проводником в экскурсии на уровень глубокого понимания алгоритма нахождения НОДа в шестом классе.
Нахождение наибольшего общего делителя (НОД) в математике 6 класс Мерзляк
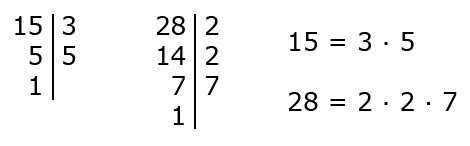
Определение НОД:
НОД двух чисел является наибольшим числом, которое одновременно является делителем обоих этих чисел. НОД является важным математическим понятием, используемым в различных задачах, таких как упрощение дробей и решение уравнений.
Методы нахождения НОД:
В этом разделе мы рассмотрим два основных метода нахождения НОД - метод деления и метод простых чисел. Метод деления основан на последовательном делении двух чисел, чтобы найти их общий делитель. Метод простых чисел основан на разложении чисел на простые множители и нахождении общих простых множителей.
Мы представим вам примеры каждого из этих методов, чтобы вы могли лучше понять, как они работают и как применить их на практике. Понимание этих методов поможет вам справиться с задачами, связанными с НОД в математике 6 класса Мерзляк.
Важно понимать, что нахождение НОД является важным шагом в решении различных задач, и эти методы помогут вам освоить этот концепт и применить его на практике.
Изучение концепции наибольшего общего делителя

В данном разделе мы рассмотрим и обсудим основное понятие в математике, которое называется Наибольший Общий Делитель (НОД). Научимся понимать сущность и значение НОД, а также изучим методы его определения и применение в различных задачах.
Наибольший Общий Делитель (НОД) - это математическое понятие, которое используется для нахождения наибольшего числа, которое делится на заданные числа без остатка. В результате нахождения НОД мы получаем наибольшее общее значение, которое является общим делителем для всех заданных чисел.
Для практического определения НОД существуют различные методы, такие как метод простых делителей, метод Эвклида и др. Каждый из них имеет свои преимущества и может быть использован в зависимости от задачи. Для нахождения НОД необходимо анализировать числовые значения и искать их общий делитель, который будет наибольшим.
Понимание и применение понятия НОД являются важной частью математического образования, так как они широко используются в различных областях, включая алгебру, геометрию, теорию чисел и другие. Знание НОД позволяет решать сложные задачи, анализировать числовые значения и находить общие закономерности.
Стратегия нахождения наибольшего общего делителя в шестом классе Мерзляк: пошаговое руководство

Шаг 1: Разложение чисел на простые множители: чтобы найти НОД двух или более чисел, нужно разложить их на простые множители. Простые числа - это числа, которые делятся только на себя и на единицу. Разложение чисел на простые множители поможет вам найти общие множители и использовать их для определения НОД.
Шаг 2: Выявление общих множителей: после разложения чисел на простые множители, следующий шаг - выявить общие множители. Общие множители - это простые множители, которые встречаются в разложении обоих чисел. Они являются основой для определения НОД.
Шаг 3: Определение НОД: после выявления общих множителей, нужно выбрать наибольший общий множитель из них. Это будет НОД исходных чисел.
Пример: Разложим числа 24 и 36 на простые множители: 24 = 2 * 2 * 2 * 3, 36 = 2 * 2 *3 * 3. Общие множители: 2 * 2 * 3 = 12. Таким образом, НОД(24, 36) = 12.
Используя этот пошаговый подход, вы сможете легко находить НОД любых чисел в шестом классе. Помните, что нахождение НОД помогает нам сократить дроби, решить задачи с делимостью и многие другие математические задачи.
Примеры работы с наибольшим общим делителем в математике 6 класса Мерзляк

В данном разделе рассмотрим практические примеры поиска наибольшего общего делителя (НОД) в математике 6 класса по методам, указанным в учебнике Мерзляк. Материал будет представлен в виде шаговых инструкций и пошаговых примеров, что позволит лучше освоить данную тему и научиться применять соответствующие методы расчетов.
1. Нахождение НОД с помощью разложения чисел на простые множители
Первый метод заключается в разложении двух чисел на простые множители и последующем поиске общих простых множителей. Затем НОД вычисляется путем перемножения найденных общих множителей.
- Шаг 1: Разложите первое и второе число на простые множители.
- Шаг 2: Найдите общие простые множители.
- Шаг 3: Перемножьте найденные общие множители, чтобы получить НОД.
Рассмотрим пример для более наглядного представления. Пусть первое число равно 24, а второе число - 36.
- Шаг 1: Разложим 24 на простые множители: 2 * 2 * 2 * 3.
- Шаг 1: Разложим 36 на простые множители: 2 * 2 * 3 * 3.
- Шаг 2: Найдем общие простые множители: 2 * 2 * 3 = 12.
- Шаг 3: НОД(24, 36) = 12.
2. Нахождение НОД с помощью алгоритма Евклида
Второй метод для нахождения НОД основан на использовании алгоритма Евклида. Этот алгоритм заключается в последовательном делении двух чисел до тех пор, пока не получится остаток равный нулю. НОД равен предыдущему ненулевому остатку.
- Шаг 1: Разделите большее число на меньшее.
- Шаг 2: Остаток от деления равен нулю?
- Шаг 3: Если остаток не равен нулю, то используйте остаток вместо большего числа и повторите шаги 1-3.
- Шаг 4: НОД равен предыдущему ненулевому остатку.
Рассмотрим пример. Пусть первое число равно 48, а второе число - 36.
- Шаг 1: Разделим 48 на 36: 48 / 36 = 1 (остаток 12).
- Шаг 2: Остаток равен нулю? Нет, переходим к следующему шагу.
- Шаг 3: Подставим остаток 12 вместо большего числа и повторим шаги 1-3: 36 / 12 = 3 (остаток 0).
- Шаг 4: НОД(48, 36) = 12.
Вопрос-ответ

Что такое нод в математике?
НОД (наибольший общий делитель) - это наибольшее число, на которое делятся два или более числа без остатка. Он является одним из важных понятий в математике и используется для решения различных задач.
Как найти НОД двух чисел?
Существует несколько способов нахождения НОДа двух чисел. Один из самых простых способов - это разложение чисел на простые множители и нахождение их общих множителей. Затем НОДом будет являться произведение этих общих множителей.



