В ходе математических расчетов и анализа числовых последовательностей часто возникает необходимость определить некоторое наименьшее общее свойство. Одним из таких свойств является наименьший общий делитель, который определяет наименьшее число, на которое делятся два заданных числа. Определение наименьшего общего делителя играет важную роль в теории чисел и нахождении рациональных чисел.
Решение задач на нахождение наименьшего общего делителя требует применения специальных методов и алгоритмов, которые не только учитывают числовые значения, но и принимают во внимание особенности их взаимного расположения. Чтобы достичь наиболее точного результата, необходимо использовать устойчивые методы, которые учитывают все возможные варианты и исключают случаи искажений.
Важно отметить, что нахождение наименьшего общего делителя может иметь практическое применение в различных областях, включая алгоритмы шифрования, теорию вероятности, а также в компьютерных и инженерных расчетах. Методы решения задач на наименьший общий делитель позволяют нам точно определить наименьшую величину, которая объединяет два числа и отражает их общие свойства и взаимосвязь.
Метод Евклида: эффективный способ нахождения наименьшего общего делителя

Одной из основных особенностей метода Евклида является его универсальность, так как он может применяться для нахождения НОД любых чисел, включая как простые числа, так и большие числа. Для использования метода Евклида не требуется знание факторизаций чисел или трудоемких вычислений.
Используя метод Евклида, можно найти наименьший общий делитель двух чисел быстро и эффективно. Алгоритм прост и основан на постоянном делении двух чисел до тех пор, пока не будет достигнут НОД. Этот процесс повторяется до тех пор, пока одно из чисел не станет равным 0. Когда это происходит, другое число будет являться наименьшим общим делителем.
Применение метода Евклида может быть полезно в различных сферах, включая математику, информатику, криптографию и другие области. Нахождение наименьшего общего делителя имеет важное значение для выполнения различных арифметических операций над дробями, а также для решения задач, связанных с простыми числами, криптографическими ключами и многими другими.
- Преимущества метода Евклида:
- Простота и надежность алгоритма;
- Высокая скорость вычислений;
- Универсальность применения для различных чисел и задач.
Общее понимание метода Евклида и его применение при поиске наименьшего общего делителя двух чисел позволяет быстро и эффективно находить НОД, что может быть полезно в различных областях и задачах, связанных с арифметическими операциями и криптографией.
Принцип и функционирование алгоритма Евклида
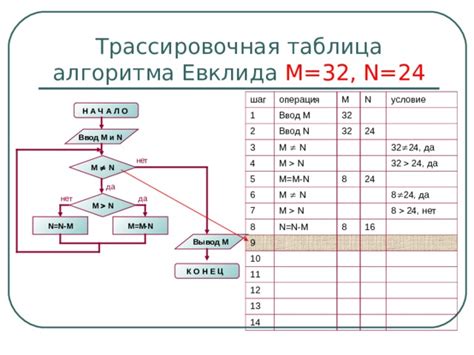
Метод Евклида представляет собой один из способов определения наименьшего общего делителя двух чисел и основывается на простом и универсальном принципе. Этот принцип заключается в поиске общего делителя чисел через последовательное вычитание одного числа из другого до тех пор, пока не будет достигнуто равенство. Таким образом, метод Евклида осуществляет поиск наименьшего общего делителя путем итеративного применения операции вычитания.
Ключевым моментом в применении алгоритма Евклида является соответствие его свойствам аддитивности и делимости. Именно поэтому данный метод универсален и может применяться для любых целых чисел без ограничений. Эта универсальность метода позволяет использовать его для нахождения наименьшего общего делителя как двух положительных, так и отрицательных чисел.
Важно отметить, что поиск наименьшего общего делителя с использованием метода Евклида является эффективным способом решения задачи. В сравнении с другими методами, основанными на факторизации чисел или переборе простых делителей, алгоритм Евклида обладает значительно меньшей вычислительной сложностью и может быть применен для чисел любой величины.
Таким образом, метод Евклида представляет собой действенный способ нахождения наименьшего общего делителя двух чисел, основанный на простом и универсальном принципе последовательного вычитания. Использование данного метода обеспечивает эффективность, универсальность и вычислительную простоту, что делает его часто используемым в различных математических и программных задачах.
Применение алгоритма Евклида для определения наименьшего общего делителя пары чисел

Простыми словами можно описать процесс следующим образом: мы берем два числа и повторяем следующие шаги: находим остаток от деления большего числа на меньшее число, затем заменяем большее число остатком и повторяем процесс до тех пор, пока не получим нулевой остаток. В этот момент полученное ненулевое число становится наименьшим общим делителем.
Применение алгоритма Евклида обладает несколькими преимуществами, такими как простота реализации и высокая эффективность. Его время исполнения все время улучшается с увеличением размеров чисел, что делает его предпочтительным методом для определения наименьшего общего делителя в практических случаях.
- Преимущества использования алгоритма Евклида:
- Простота реализации;
- Высокая эффективность в сравнении с другими методами;
- Улучшение времени исполнения с увеличением размеров чисел;
- Общий применимость к различным задачам и ситуациям, где необходимо найти наименьший общий делитель.
Альтернативные подходы к определению наименьшего общего множителя чисел

В данном разделе рассмотрим другие способы определения наименьшего общего множителя (НОМ) двух чисел, кроме уже известных методов. Ряд предлагаемых альтернативных подходов позволят найти НОМ двух чисел с использованием неконвенциональных методов и алгоритмов.
Первый подход основывается на поиске общих множителей чисел и их дальнейшей факторизации. Используя различные методы разложения чисел на простые множители, можно найти общие простые делители исходных чисел. После этого производится перемножение найденных простых делителей и получается НОМ.
Второй подход основан на применении ряда арифметических операций над исходными числами. Один из таких подходов - метод итераций над остатками. Идея заключается в последовательном вычислении остатков от деления одного числа на другое и дальнейшего использования этих остатков для нахождения НОМ. При этом используются различные операции, такие как вычитание и деление.
Третий подход предлагает использование арифметических прогрессий для определения НОМ. Идея состоит в том, чтобы найти наименьшее число, которое делится на оба исходных числа и заданный НОМ. Для этого используется принцип арифметической прогрессии и уравнения с неизвестными коэффициентами.
Каждый из предложенных альтернативных методов имеет свои уникальные особенности и может быть применен в различных ситуациях. Выбор подхода зависит от специфики задачи и требуемой эффективности вычислений.
Вопрос-ответ

Как найти наименьший общий делитель двух чисел?
Для нахождения наименьшего общего делителя двух чисел можно использовать несколько методов. Один из самых простых способов - применение алгоритма Евклида. Сначала нужно найти остаток от деления большего числа на меньшее. Затем найти остаток от деления предыдущего остатка на результат, и так далее, пока не получим нулевой остаток. На последнем шаге наименьший общий делитель будет равен предыдущему ненулевому остатку.
Какой метод эффективнее для поиска наименьшего общего делителя?
Один из самых эффективных методов для поиска наименьшего общего делителя - метод Евклида. В отличие от перебора всех возможных делителей чисел, алгоритм Евклида позволяет быстро и эффективно находить НОД. Алгоритм работает за логарифмическое время в зависимости от величины чисел и дает точный результат.
Каким образом можно применить рекурсию для нахождения НОД?
Для решения задачи нахождения НОД с помощью рекурсии в алгоритме Евклида, нужно определить базовый случай - возвращать делитель, если второе число равно нулю. В остальных случаях вызывать функцию рекурсивно, передавая в нее второе число и остаток от деления первого числа на второе.
Какой алгоритм можно использовать для поиска НОД трех и более чисел?
Для поиска НОД трех и более чисел можно применить расширенный алгоритм Евклида. Он основан на последовательном применении обычного алгоритма Евклида к парам чисел до тех пор, пока не останется только одно число - НОД. Расширенный алгоритм Евклида позволяет также вычислить коэффициенты Безо для каждой пары чисел, что может быть полезно в некоторых задачах, связанных с диофантовыми уравнениями.
Какие еще есть методы для нахождения наименьшего общего делителя?
Помимо алгоритма Евклида, существуют и другие методы для нахождения наименьшего общего делителя. Один из них - простой перебор делителей чисел. Этот метод состоит в последовательной проверке всех чисел от 2 до минимального числа из пары, на делимость обоих чисел. Когда найдется первый общий делитель, он будет наименьшим общим делителем. Однако этот метод неэффективен для больших чисел, так как время его выполнения зависит от самого числа.
Какой метод можно использовать для поиска наименьшего общего делителя двух чисел?
Для поиска наименьшего общего делителя двух чисел можно использовать метод Евклида.
Как работает метод Евклида для поиска наименьшего общего делителя двух чисел?
Метод Евклида основан на простом алгоритме, который заключается в последовательном нахождении остатка от деления одного числа на другое и замене этих чисел друг на друга. По сути, метод заключается в повторении этого процесса до тех пор, пока не будет достигнуто нулевое значение остатка. В конечном итоге, когда остаток становится равным нулю, последнее ненулевое число является наименьшим общим делителем.



