Для осуществления нашей жизни нам часто приходится принимать решения. Некоторые из них могут быть незначительными и не требовать особого внимания, но существуют и такие, которые имеют глубокий отпечаток на нашей жизни. И как бы ни было трудно, взвешивание всех предоставленных вариантов и выбор правильного пути может стать сложным процессом.
Однако существует эффективный и простой инструмент, который помогает нам систематизировать и анализировать доступную информацию и принимать обоснованные решения. Этот инструмент известен как квадрат Декарта. Он назван в честь своего создателя, французского философа и математика Рене Декарта, и представляет собой наглядное средство для оценки преимуществ и недостатков различных вариантов.
Квадрат Декарта включает в себя две оси: горизонтальную и вертикальную. Горизонтальная ось отображает положительные и отрицательные аспекты каждого варианта, а вертикальная ось - важность каждого из них. Объединив эти две составляющие, мы можем найти наиболее обоснованный и оптимальный вариант для нашего решения.
Важно отметить, что квадрат Декарта не является единственным методом принятия решений, но его простая и понятная структура делает его популярным и эффективным инструментом.
Понятие квадрата Декарта: основы и принципы
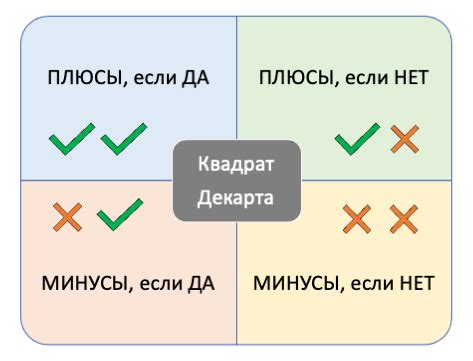
В данном разделе мы исследуем фундаментальное понятие, которое может оказать существенное влияние на принятие решений в различных сферах жизни. Мы рассмотрим основные идеи, лежащие в основе квадрата Декарта, и принципы его применения.
Перед нами стоит задача понять, как осмысленно взаимодействовать с информацией, строить свои мысли и принимать взвешенные решения. Квадрат Декарта представляет собой инструмент, который помогает нам систематизировать и оценивать различные факторы, учитывать их взаимосвязь и влияние на наши решения.
- Одной из основных идей квадрата Декарта является его четырехквадрантная структура, где каждый квадрант представляет собой определенный сегмент информации. Эти сегменты обозначают различные аспекты проблемы или решения, исходя из которых мы можем анализировать и принимать решения.
- Важным принципом использования квадрата Декарта является учет взаимосвязи и влияние каждого аспекта на другие. Взаимодействие между квадрантами позволяет нам более глубоко понять сложность проблемы и определить наиболее эффективные решения.
- Квадрат Декарта также помогает нам идентифицировать приоритеты и установить вес каждого аспекта для достижения наилучшего результата. Оценка значимости и влияния каждого квадранта позволяет более обоснованно определить последовательность и приоритеты при принятии решений.
- Использование квадрата Декарта подразумевает систематический подход к анализу и принятию решений. Он помогает структурировать информацию, оценивать аспекты проблемы и выбирать оптимальные решения, основываясь на более полной и объективной картине.
Разумное использование квадрата Декарта может существенно улучшить наши навыки принятия решений в различных ситуациях. Используя этот подход, мы сможем более точно анализировать информацию, выявлять причинно-следственные связи и принимать обоснованные и взвешенные решения, обеспечивая устойчивое развитие и достижение поставленных целей.
Декартово произведение: путь к прозорливости в принятии решений

На протяжении веков декартово произведение доказало свою эффективность в различных областях, включая логику, философию, информатику и другие науки. Это мощный инструмент, который помогает нам разбить сложную проблему на более простые компоненты и анализировать их по отдельности. Это позволяет нам получить более ясное представление о взаимосвязи различных факторов, что ведет к улучшенному пониманию ситуации и принятию более обоснованных решений.
| Преимущества декартова произведения в принятии решений: |
|---|
| 1. Разрешение сложных проблем. Декартово произведение позволяет нам разбить сложную проблему на более простые компоненты, что делает ее более управляемой и понятной. |
| 2. Объективность. С помощью декартова произведения мы можем провести объективный анализ различных факторов и взаимосвязей, что поможет нам избежать предвзятых или искаженных представлений и принять решение на основе фактов и данных. |
| 3. Систематичность. Декартово произведение предоставляет нам систематический подход к принятию решений, позволяя нам рассмотреть все возможные комбинации и варианты взаимодействия между факторами. |
| 4. Визуализация. С помощью декартова произведения мы можем визуально представить информацию и взаимосвязи в виде таблицы или диаграммы, что делает ее более понятной и легкой для анализа. |
Таким образом, декартово произведение не только предоставляет нам эффективный метод разбиения сложной проблемы на простые компоненты, но и позволяет нам анализировать эти компоненты отдельно, взаимодействие между ними и их влияние на принятие решений. Используя эту мощную концепцию, мы можем повысить нашу прозорливость и принимать более обоснованные решения в самых разнообразных ситуациях.
Алгоритм анализа проблемы с помощью картины Декарта

В этом разделе мы рассмотрим пошаговый алгоритм использования картины Декарта для анализа и решения проблемной ситуации. Декарта можно воспринимать как инструмент, который помогает разложить сложную проблему на более простые составляющие, визуализировать их в виде картины и последовательно анализировать каждый элемент для получения итогового решения.
Шаг 1: Определение основной проблемы или вопроса, требующего решения. Необходимо ясно сформулировать суть проблемы в виде вопроса, чтобы иметь точку отсчета для дальнейшего анализа.
Шаг 2: Разделение проблемы на две основные переменные или факторы. Декарта представляет собой двумерную таблицу, где ось X и ось Y представляют различные факторы или переменные, влияющие на проблему. Необходимо определить два наиболее существенных фактора, которые нужно анализировать для получения полной картины проблемы.
Шаг 3: Определение возможных значений каждой переменной. Для каждой переменной необходимо выделить диапазон возможных значений, которые могут влиять на проблему. Это поможет учесть все возможные сценарии и обеспечить комплексный анализ.
Шаг 4: Заполнение квадрата Декарта значениями переменных. Создайте таблицу, где на оси X указываются значения одной переменной, на оси Y - значения второй переменной. Заполните таблицу соответствующими значениями, отражающими их взаимосвязь.
Шаг 5: Анализ картины и идентификация закономерностей. Изучите заполненную таблицу и проанализируйте взаимосвязь между значениями переменных. Обратите внимание на возможные закономерности, тренды или противоречия, которые могут иметь прямое отношение к проблеме.
Шаг 6: Процесс принятия решения. На основе анализа картины Декарта и выявления закономерностей, приступите к разработке возможных решений. Используйте информацию, полученную из таблицы, чтобы принять взвешенное и обоснованное решение, учитывая влияние каждой переменной на итоговый результат.
Шаг 7: Оценка эффективности решения. После принятия решения и его реализации, необходимо оценить его эффективность. Проведите анализ, чтобы определить, насколько решение помогло в решении проблемы и достижении поставленных целей.
Используя этот алгоритм анализа проблемы с помощью картины Декарта, вы сможете систематически разложить сложную проблему на составляющие, изучить их взаимосвязи и принять взвешенное решение на основе полученных данных.
| Переменная 1 | Переменная 2 | |
|---|---|---|
| Значение 1 | ... | ... |
| Значение 2 | ... | ... |
Разбор сложных задач: эффективное применение квадрата Декарта

Концепция Квадрата Декарта решений
Квадрат Декарта является методом, основанном на принципе разделения проблемы на отдельные аспекты и структурировании их в соответствующих категориях. Затем каждый аспект можно проанализировать, определить возможные решения и выбрать наиболее оптимальный вариант действий.
Декартов квадрант – это не только способ глубокого понимания сложной проблемы, но и возможность оценить все факторы, которые могут повлиять на результат принимаемого решения.
Процесс анализа задач с использованием Квадрата Декарта
Для успешного использования Квадрата Декарта нужно последовательно пройти через несколько этапов. Сначала необходимо определить основные аспекты или факторы, которые влияют на решение данной задачи. Затем эти аспекты разделются на две основные категории: положительные и отрицательные. После этого каждый аспект проходит анализ и оценку в зависимости от его важности и воздействия на результат. В конечном итоге, с помощью Квадрата Декарта можно найти оптимальное решение, избегая возможных непредвиденных последствий.
Использование Квадрата Декарта для разбора сложных задач позволяет нам более глубоко понять проблему, структурировать информацию и принять взвешенное решение с учетом всех важных факторов. Этот метод поможет нам справиться с самыми сложными ситуациями и достичь наилучшего итогового результата.
Роли направления и значения в координатной плоскости и их воздействие на принятие решений
Одна из осей, горизонтальная ось абсцисс, представляет одну переменную или параметр, в то время как вертикальная ось ординат – вторую переменную или параметр. Направление осей имеет значение, которое влияет на принятые решения и интерпретацию данных. Положительное направление на горизонтальной оси указывает на возрастание значения переменной, в то время как положительное направление на вертикальной оси указывает на увеличение значения второй переменной.
Знание роли осей в квадрате Декарта помогает нам проанализировать данные и принять обоснованные решения. Положение точек на графике и их отношения к осям позволяют нам определить тренды, гипотезы и зависимости между переменными. Мы можем использовать координатную плоскость для сравнения результатов, выявления предпочтений и повышения понимания информации.
Принятие решений с учетом влияния осей в системе координат

Использование системы координат на плоскости для анализа и принятия решений предоставляет возможность учитывать влияние осей и их отношений друг к другу. Важно понимать, как оси влияют на наше восприятие данных и как это может повлиять на наши решения.
Оси в квадрате Декарта представляют различные факторы или переменные, которые могут быть взяты во внимание при принятии решений. Каждая ось имеет свое значение и вклад в решение, их взаимное положение и направление отражают взаимосвязь и степень влияния этих факторов друг на друга.
Возможности анализа осей в системе координат позволяют:
- Оценить влияние каждой оси на общую картину и результат принимаемого решения. Это помогает понять, как каждый фактор влияет на конечный результат и какие аспекты следует учитывать при принятии решений.
- Идентифицировать сильные и слабые стороны каждой оси. Анализ осей позволяет определить, какие факторы имеют наибольшую важность и какие могут быть пренебрежены, а также выявить возможные риски при использовании определенной оси при принятии решений.
- Найти и оптимизировать взаимосвязи между осями. Понимание взаимодействия между осью X и Y, например, помогает найти оптимальное сочетание переменных, которые могут привести к наилучшему результату.
- Предсказывать и оптимизировать будущие тренды и изменения на основе данных, полученных из системы координат. Анализ осей позволяет выявить тенденции и паттерны, которые помогут принять более информированные решения в будущем.
Анализ и учет влияния осей в системе координат являются важной составляющей принятия решений. Он позволяет сделать наблюдения более объективными и обеспечить более точные и информированные решения, которые учитывают взаимосвязи и важность каждого фактора.
Вопрос-ответ

Как использовать квадрат декарта для принятия решений?
Квадрат Декарта - это графическое представление, которое помогает структурировать проблему и принимать рациональные решения. Для его использования, необходимо разделить пространство на четыре квадранта и анализировать факторы, влияющие на принятие решения. На основе этого анализа можно сделать обоснованный выбор и решить проблему в наилучшем для вас варианте.
Какие факторы следует учитывать при использовании квадрата Декарта для принятия решений?
При использовании квадрата Декарта для принятия решений, необходимо учитывать различные факторы. В первом квадранте следует оценить важность проблемы и ее срочность. Во втором квадранте следует рассмотреть все возможные варианты решений. В третьем квадранте следует оценить риски и негативные последствия принятого решения. В четвертом квадранте следует оценить потенциальные выгоды и плюсы, которые принесет решение проблемы.
Можете ли вы дать пример использования квадрата Декарта для принятия решений?
Конечно! Представим, что у вас есть задача выбрать новую работу. Вы можете использовать квадрат Декарта, чтобы помочь с принятием этого решения. В первом квадранте вы можете учесть срочность задачи и понять, насколько быстро вам нужно найти новую работу. Во втором квадранте вы можете рассмотреть различные варианты работы, рефлексируя о своих интересах и квалификации. В третьем квадранте вы можете сделать анализ рисков, учитывая потенциальные негативные последствия смены работы. В четвертом квадранте вы можете оценить потенциальные выгоды и преимущества, которые может принести новая работа, такие как большая оплата или профессиональный рост. На основе этого анализа вы сможете принять обоснованное решение о том, какую работу выбрать.



