Вас интересует вычисление площади фигур с помощью калькулятора? Мы предлагаем простое и эффективное решение для расчета площади треугольника по заданным сторонам. Благодаря нашему онлайн-калькулятору вы получите быстрый и точный результат без лишних затруднений.
Наш инструмент основывается на математических принципах и использует формулу, основанную на длинах трех сторон треугольника. Благодаря этому вы сможете рассчитать площадь треугольника, не прибегая к сложным и времязатратным вычислениям вручную.
Пользуясь нашим калькулятором, вы сможете применить свои знания геометрии и математики на практике. Более того, вы получите возможность быстро и безошибочно определить площадь треугольника по заданным сторонам, что может быть полезно в различных сферах жизни и профессиональной деятельности.
Использование инструмента для вычисления площади треугольника по трем его сторонам
Рассмотрим способ использования специального инструмента, который позволяет рассчитать площадь треугольника, зная длины всех его сторон. Данная техника основывается на формуле Герона и требует ввода значений сторон треугольника в специальный калькулятор для получения точных результатов.
Для начала определимся со значениями, которые нам потребуются. В случае если вы знаете длины сторон треугольника, вам рекомендуется использовать этот инструмент для вычисления его площади, так как он обеспечивает точность и надежность результатов.
При использовании калькулятора для вычисления площади треугольника по трем сторонам важно следовать определенной последовательности. Сначала введите длину первой стороны, затем введите значения остальных двух сторон в соответствующие поля. После ввода всех необходимых данных, нажмите кнопку "Рассчитать", чтобы получить площадь треугольника.
Помните, что для получения корректного результата необходимо правильно измерить и ввести значения сторон треугольника, а также следовать указанным инструкциям. Использование этого калькулятора позволит вам получить быстрые и точные результаты, избегая ошибок, связанных с мануальным вычислением площади треугольника.
Основные понятия в расчете площади треугольника по трем сторонам
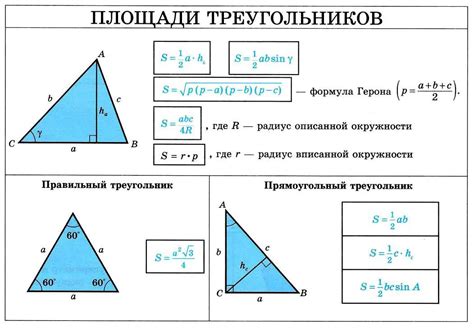
В процессе расчета площади треугольника по трем сторонам необходимо освоить несколько основных понятий, которые помогут понять суть задачи и правильно применять соответствующую формулу. Разберемся с определениями, чтобы быть уверенными в правильности решаемой задачи.
- Треугольник: геометрическая фигура, образованная тремя отрезками, называемыми сторонами треугольника.
- Сторона: отрезок, который соединяет две вершины треугольника.
- Площадь: мера поверхности треугольника, которая позволяет вычислить его размер в единицах площади.
- Формула: математическое выражение, используемое для нахождения искомого значения площади треугольника по заданным сторонам.
Имея представление об этих понятиях, вы сможете эффективно использовать калькулятор для нахождения площади треугольника по его сторонам. В следующих разделах мы подробно рассмотрим каждый этап расчета и предоставим практические примеры для лучшего понимания.
Необходимые формулы для вычисления площади треугольника
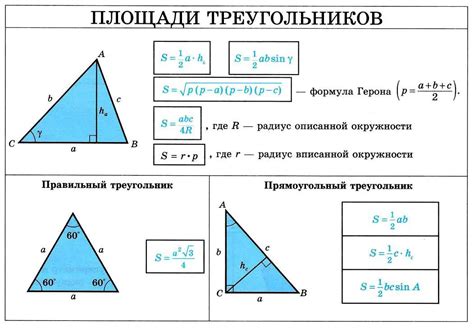
В этом разделе будут представлены основные математические формулы, которые позволят вам вычислить площадь треугольника исходя из известных сторон.
- Формула Герона: Эта формула основана на полупериметре треугольника и разности длин его сторон. С ее помощью можно рассчитать площадь треугольника без знания высоты.
- Формула полупроизведений: Для расчета площади треугольника по сторонам можно использовать эту формулу, которая основана на произведении сторон треугольника и синуса угла между ними.
- Формула трех векторов: Если известны координаты вершин треугольника, можно использовать эту формулу, основанную на нахождении площади параллелограмма, образованного векторами сторон треугольника.
Знание этих формул позволит вам справиться с расчетами площади треугольника без необходимости использования специальных калькуляторов или онлайн-инструментов.
Проверка условий возможности построения треугольника
В данном разделе рассмотрим условия, при которых можно построить треугольник на основе заданных значений трех его сторон.
Определим основные понятия:
- Стороны треугольника - это отрезки, соединяющие вершины треугольника.
- Треугольник - это геометрическая фигура, образованная тремя отрезками, которые образуют замкнутую ломаную линию без самопересечений.
При построении треугольника важно учитывать следующие условия:
| Условие | Описание |
|---|---|
| Условие существования | Сумма любых двух сторон треугольника должна быть больше третьей стороны. |
| Условие неравенства треугольника | Summa любых двух сторон треугольника должна быть меньше суммы оставшейся третьей стороны. |
| Условие положительности сторон | Длина каждой стороны треугольника должна быть больше нуля. |
Если все указанные условия выполнены, то треугольник можно построить на основе заданных значений его сторон. Если хотя бы одно условие не выполняется, то треугольник с такими сторонами невозможно построить.
Ввод данных о размерах трех сторон треугольника в калькуляторе
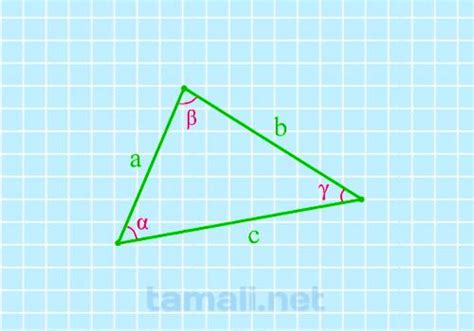
В данном разделе будет рассмотрен процесс ввода данных о размерах трех сторон треугольника в калькуляторе, с помощью которого можно определить площадь данной фигуры. Для выполнения расчетов необходимо внести значения каждой из сторон треугольника в соответствующие поля калькулятора.
| Сторона A: | Введите значение стороны A треугольника: |
| Сторона B: | Введите значение стороны B треугольника: |
| Сторона C: | Введите значение стороны C треугольника: |
Обратите внимание, что вводимые значения должны быть вещественными числами и не могут быть отрицательными. Также необходимо учесть условие существования треугольника, согласно которому сумма двух любых сторон треугольника должна быть больше третьей стороны.
Для более точного результата рекомендуется использовать точные значения сторон треугольника. В случае необходимости округления числа, это следует сделать до ввода данных в калькулятор.
После внесения значений всех сторон треугольника, нажмите кнопку "Рассчитать" или соответствующий аналогичный элемент управления, чтобы получить расчетную площадь данной фигуры.
Анализ и корректное заполнение полей калькулятора: руководство пользователя
Для получения точного и верного результата при вычислении площади треугольника по его трём сторонам с использованием калькулятора, необходимо правильно заполнить все поля инструмента.
1. Внимательно изучите функционал калькулятора и его интерфейс. Понимание, какие поля заполнять и какие значения вводить, поможет избежать ошибок в процессе расчётов.
2. Проверьте, что значения, которые вы собираетесь ввести, соответствуют контексту. Помните, что длины сторон треугольника должны быть положительными числами без обозначений направления, таких как "+", "-" или "0".
3. Используйте подходящие единицы измерения для ввода значений. Например, если треугольник имеет стороны в сантиметрах, убедитесь, что вы вводите значения в сантиметрах, а не в метрах или дюймах.
4. Если вам необходимо вычислить площадь треугольника с использованием десятичных чисел, учтите, что разделитель десятичных знаков может быть запятой или точкой, в зависимости от выбранной системы десятичных разделителей.
5. В случае, если калькулятор предлагает выбор способа вычисления площади треугольника (например, формулы Герона или формулы полупериметра), убедитесь, что вы правильно выбрали соответствующие опции или указали параметры для вычислений.
Внимательность и аккуратность при заполнении полей калькулятора гарантируют точность результата. Помните, что важно следовать указанным инструкциям и правильно интерпретировать значения, чтобы получить правильную площадь треугольника.
Результат вычисления области треугольника, определенного по длинам его сторон
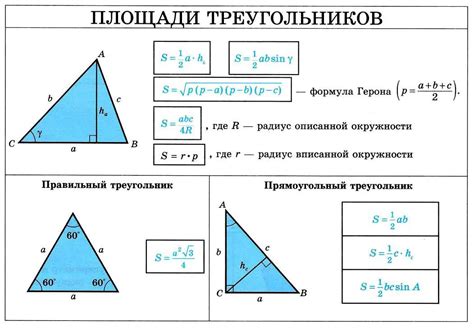
Раздел "Результат расчета площади треугольника" представляет собой подробное описание процесса вычисления площади треугольника, основанное на полученных длинах его сторон. В этом разделе представлена информация о необходимых формулах и алгоритмах, которые позволяют получить точные значения площади треугольника без использования калькулятора. Более того, здесь также будет рассмотрено несколько примеров вычисления площади треугольника на основе длин его сторон, чтобы помочь читателю лучше понять процесс.
Дополнительные возможности инструмента для нахождения площади треугольника
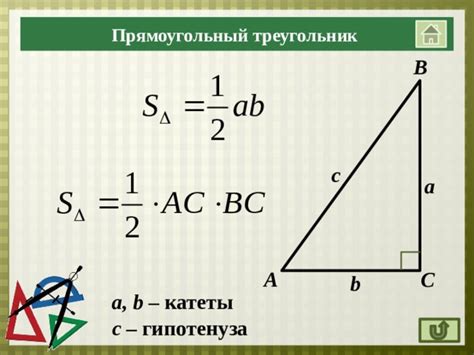
Помимо основной функции расчета площади треугольника по трем сторонам, доступны и другие полезные инструменты. Эти дополнительные функции позволяют упростить работу с треугольниками и получить дополнительную информацию о них.
1. Нахождение периметра: Калькулятор предоставляет возможность вычислить периметр треугольника, основываясь на заданных значениях его сторон. Периметр является суммой всех трех сторон и играет важную роль в изучении свойств треугольников.
2. Определение типа треугольника: На основе значений сторон калькулятор может определить, какому классу треугольников принадлежит заданный треугольник. Это может быть равносторонний, равнобедренный или разносторонний треугольник. Знание типа треугольника позволяет понять его особенности и свойства.
3. Конструктор треугольника: Калькулятор может помочь построить треугольник на экране, исходя из заданных значений его сторон. Это позволяет визуализировать треугольник и лучше понять его геометрическую форму.
4. Расчет углов: Используя информацию о сторонах треугольника, калькулятор позволяет определить значения углов. Это особенно полезно при изучении геометрии треугольников и решении связанных с ними задач.
Эти дополнительные функции позволяют сделать работу с треугольниками более удобной и эффективной. Они помогают получить дополнительную информацию о треугольнике, которая может быть полезной при его изучении или решении задач, связанных с этой геометрической формой.
Расчет площади треугольника вручную без использования вычислительных средств
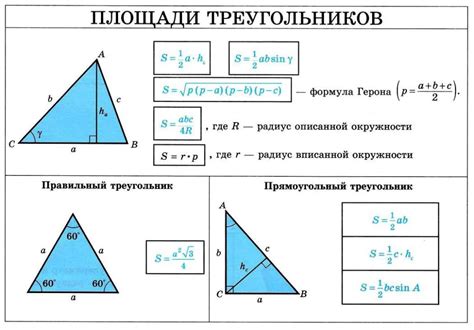
Этот раздел посвящен методам ручного вычисления площади треугольника без использования калькулятора и других электронных средств. Здесь мы рассмотрим различные подходы и формулы, которые позволят нам определить площадь треугольника с помощью исключительно математических операций.
Вопрос-ответ

Как узнать площадь треугольника, если известны все три стороны?
Чтобы найти площадь треугольника, если известны все три стороны, можно воспользоваться формулой Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, а, b, c - длины сторон, p - полупериметр треугольника.
Какой калькулятор поможет найти площадь треугольника по трем сторонам?
Существует множество онлайн-калькуляторов, которые могут помочь вам найти площадь треугольника по трем сторонам. Просто введите значения сторон в соответствующие поля и нажмите кнопку "Рассчитать". Результат будет выведен на экран.
Что делать, если известны только длины сторон треугольника, но нет калькулятора?
Если у вас нет калькулятора, но известны длины сторон треугольника, вы можете вручную рассчитать площадь. Сначала найдите полупериметр треугольника, сложив длины всех трех сторон и разделив полученную сумму на 2. Затем воспользуйтесь формулой Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, а, b, c - длины сторон, p - полупериметр треугольника. Выполните все необходимые вычисления и найдите площадь треугольника.
Можно ли найти площадь треугольника по трем сторонам без знания их высот?
Да, можно найти площадь треугольника по трем сторонам без знания их высот. Для этого необходимо использовать формулу Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, а, b, c - длины сторон, p - полупериметр треугольника. Вычислите значения согласно формуле, и вы получите площадь треугольника.
Какое значение дает формула Герона для площади треугольника по трем сторонам?
Формула Герона для площади треугольника по трем сторонам дает точное значение площади треугольника, и она считается одним из самых точных способов нахождения площади треугольника по длинам его сторон. Однако, следует помнить, что для применения этой формулы треугольник должен быть невырожденным, то есть его стороны должны быть положительными и удовлетворять условию треугольника.
Как узнать площадь треугольника, если известны длины его сторон?
Для вычисления площади треугольника по длинам его сторон можно использовать формулу Герона. Сначала нужно вычислить полупериметр треугольника, который равен сумме длин всех его сторон, деленной на 2. Затем, применяя формулу Герона, можно найти площадь треугольника по формуле sqrt(s * (s - a) * (s - b) * (s - c)), где s - полупериметр треугольника, a, b, c - длины его сторон.



