В ходе изучения математики в школе мы неоднократно сталкиваемся с различными геометрическими фигурами и задачами, связанными с их площадями. Одной из таких фигур является трапеция, играющая важную роль в геометрических расчетах. В данной статье рассмотрим один из способов вычисления площади трапеции, основанный на счете клеток.
Трапеция - это плоская фигура, имеющая параллельные основания и стороны, причем одно основание (нижнее) обычно длиннее другого (верхнего). Расчет площади трапеции особенно актуален в жизни: это может быть использовано при строительстве кровли, архитектурном и дизайнерском проектировании, а также в ряде других задач.
Особенностью данного метода расчета площади трапеции является использование клеток. При этом мы разбиваем трапецию на прямоугольники размером в одну клетку и считаем их количество. Такой способ весьма гибок и доступен даже для учащихся средней школы, позволяя легко представить абстрактную фигуру в понятной форме.
Основные параметры трапеции: понятие, структура и свойства
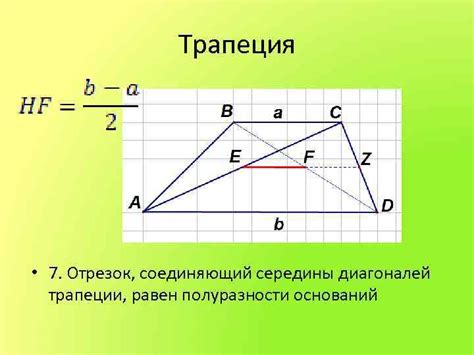
Основа Параллельные стороны трапеции, обозначаемые как основы, играют ключевую роль в её структуре. Они являются двумя строго параллельными линиями, которые способны гарантировать определенность формы фигуры и связывать её все остальные элементы. Основы обычно обозначаются буквами a и b. | Боковые стороны Боковые стороны трапеции соединяют каждую из вершин основы. Они могут быть как параллельными, так и непараллельными, добавляя разнообразие и гибкость в конструкцию трапеции. Боковые стороны обычно обозначаются буквами c и d. |
Высота Высота трапеции – это перпендикуляр, опущенный из одного края трапеции на противоположное основание. Она является важным параметром для расчета площади трапеции и определения её характеристик. Высота обычно обозначается буквой h. | Диагонали Диагонали трапеции – это отрезки, соединяющие противоположные углы. Они могут быть непараллельными, а их связь с другими сторонами трапеции определяет её форму и свойства. Обозначаются буквами e и f. |
Изучение этих основных параметров и показателей трапеции поможет вам лучше разобраться в её структуре и использовании в различных задачах, включая определение площади трапеции на клетчатой плоскости. Теперь, имея понимание основных определений и свойств трапеции, вы сможете приступить к решению более сложных задач и применению геометрических знаний в практике.
Определение и параметры трапеции

У трапеции есть несколько параметров, о которых необходимо знать:
| Основание | Это две параллельные стороны трапеции, представляющие собой ее больший и меньший край. Они обозначаются буквами a и b. |
| Боковые стороны | Это две непараллельные стороны трапеции, соединяющие основания. Они обозначаются буквами c и d. |
| Высота | Это перпендикуляр, опущенный из вершины трапеции на основание. Обозначается буквой h. |
| Диагонали | Это отрезки, соединяющие противоположные вершины трапеции. Они обозначаются буквами p и q. |
Знание данных параметров позволяет определить и вычислить различные характеристики трапеции, включая ее площадь, периметр и другие.
Методика вычисления площади трапеции по клеткам

Для начала необходимо определить длины оснований трапеции по заданным клеткам. Основание трапеции - это горизонтальная сторона, образующаяся между двумя параллельными сторонами трапеции. Для определения длины оснований можно воспользоваться подсчетом числа клеток, лежащих на каждой из оснований.
После определения длин оснований необходимо вычислить высоту трапеции. Высота трапеции - это перпендикуляр, опущенный из одного основания на другое. Для определения высоты можно воспользоваться подсчетом числа клеток, лежащих на перпендикуляре, проведенном из одного основания на другое.
Используя полученные значения длин оснований и высоты, можно применить формулу для вычисления площади трапеции: площадь равна половине произведения суммы длин оснований на высоту. Результатом будет площадь трапеции в квадратных клетках.
Построение трапеции на координатной плоскости и определение ее площади
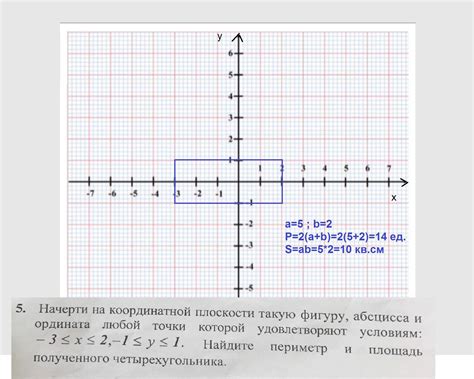
Размещение фигур на координатной плоскости предоставляет возможность анализировать и изучать геометрические формы с использованием числовых значений. В данном разделе мы рассмотрим процесс построения трапеции на координатной плоскости и определение ее площади.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие стороны – непараллельны. Одна из возможных стратегий для построения трапеции на координатной плоскости – использование координат вершин фигуры. Устанавливая точки с определенными значениями координат, можно создать трапецию и визуально представить ее форму. Например, можно определить координаты вершин трапеции и соединить их линиями для получения фигуры.
После построения трапеции на координатной плоскости, мы можем перейти к определению ее площади. Для этого можно использовать различные методы, включая применение формулы площади трапеции, которая основана на использовании высоты и средней линии. Процесс вычисления площади трапеции требует математических расчетов и использования соответствующих формул.
Примеры вычисления площади трапеции на клетчатой поверхности

В данном разделе будут представлены наглядные примеры расчета площади трапеции на клетчатой поверхности с использованием таблицы. Мы рассмотрим различные варианты трапеций и покажем, как их площадь можно определить, используя сетку из клеток. Мы расширим наши знания о геометрии и математическом моделировании, чтобы легче понять применение этих понятий на практике.
| Пример 1 | Пример 2 | Пример 3 |
|---|---|---|
| Трапеция А | Трапеция В | Трапеция С |
| 1 клетка | 2 клетки | 3 клетки |
| 2 клетки | 3 клетки | 4 клетки |
| 3 клетки | 4 клетки | 5 клеток |
В каждом из примеров мы представим трапецию с различным количеством клеток в основаниях и высоте. С помощью таблицы, где каждая клетка представляет единицу площади, мы определим общую площадь трапеции. Узнаем, как связаны клетки нашей таблицы с геометрическими показателями трапеции и как использовать эту информацию для расчета площади. Такой подход позволит нам визуализировать процесс и сделать его более понятным и удобным.
Вопрос-ответ

Как правильно найти площадь трапеции по клеткам?
Для того чтобы найти площадь трапеции по клеткам, нужно посчитать количество клеток, закрашенных внутри фигуры, и умножить это значение на площадь одной клетки.
Каким образом определить площадь трапеции в 9 классе на основании клеток?
Для определения площади трапеции в 9 классе на основании клеток, нужно выделить внутренние клетки, закрашенные внутри фигуры, и подсчитать их количество. Затем, нужно умножить это значение на площадь одной клетки, чтобы получить окончательный результат.
Каковы основные шаги для вычисления площади трапеции в 9 классе, используя клетки?
Основные шаги для вычисления площади трапеции в 9 классе, используя клетки, следующие: определить внутренние клетки, которые закрашены внутри фигуры, подсчитать их количество, а затем умножить это значение на площадь одной клетки.
Как количество клеток помогает найти площадь трапеции по клеткам в 9 классе?
Количество клеток помогает найти площадь трапеции по клеткам в 9 классе, так как оно позволяет определить, сколько клеток закрашено внутри фигуры. Умножив эту величину на площадь одной клетки, можно получить окончательную площадь трапеции.
Что нужно делать, если в трапеции, которую нужно измерить по клеткам, есть пропущенные или незакрашенные клетки?
Если в трапеции, которую нужно измерить по клеткам, есть пропущенные или незакрашенные клетки, нужно выделить только те клетки, которые полностью находятся внутри фигуры, и подсчитать их количество. Это позволит получить точную площадь трапеции.
Как можно найти площадь трапеции по клеткам в 9 классе?
Для того чтобы найти площадь трапеции по клеткам в 9 классе, необходимо знать количество клеток, занимаемых трапецией. Затем нужно умножить это количество на площадь одной клетки, которая определяется по размеру сетки или таблицы, на которой трапеция отобразилась. Если сетка имеет одинаковые клетки, то площадь одной клетки равна ее размеру вдоль одной оси, умноженному на размер вдоль другой оси. После вычисления площади одной клетки нужно умножить ее на количество клеток, занимаемых трапецией, и получить итоговую площадь трапеции.
Можно ли найти площадь трапеции по клеткам без знания ее размеров? Если да, то как?
Да, площадь трапеции по клеткам можно найти без знания ее размеров. Для этого необходимо знать количество клеток, занимаемых трапецией, и площадь одной клетки, которая может быть определена по размеру сетки или таблицы, на которой трапеция отобразилась. Зная площадь одной клетки, необходимо умножить ее на количество клеток, занимаемых трапецией, и получить итоговую площадь трапеции.



