Среди множества фигур, встречающихся в мире геометрии, треугольник без сомнения является одной из самых известных и изученных.
Однако, когда речь заходит о размещении треугольника внутри окружности, открывается дверь в удивительный мир, полный загадок и интересных открытий.
При использовании особого инструмента - циркуля, а также при помощи сновидческого воображения и быстрой мастерской руки, геометрическое искусство раскрывает свои безграничные возможности. Внутри круга, натянутого на заколки или металлический подставку, экспериментатор может создавать бесконечное количество треугольников, каждый со своим искривлением, формой и размером.
Добро пожаловать в удивительный и привлекательный мир конструкций, где геометрические формы становятся живыми и оживают под руками творца. Удивительно, как три точки, лежащие на границе окружности, могут преобразоваться в такое множество треугольников - от правильных и равнобедренных до неправильных и причудливо искаженных.
Классический метод проведения треугольника с использованием циркуля

Раздел данной статьи посвящен описанию классического метода проведения треугольника с использованием инструмента под названием циркуль. В рамках данного метода демонстрируются способы создания треугольника в окружности с использованием относительных понятий, таких как радиус, центр окружности и углы.
Построение треугольника с помощью циркуля и линейки внутри окружности

В этом разделе рассмотрим уникальный метод создания треугольника внутри окружности, используя всего лишь циркуль и линейку. Этот метод позволяет с легкостью определить вершины треугольника и построить его в круге, не прибегая к другим инструментам или усложняющим вычислениям.
Для начала понадобятся синонимы для описания требуемого предмета и процесса: определение вершин, построение формы, использование инструментов. Обозначим эти понятия как "идентификация точек", "установка фигуры", "применение средств".
При использовании циркуля и линейки, можно легко определить три точки на окружности, которые будут служить вершинами треугольника. Сначала, устанавливаем радиус посредством размещения линейки от центра окружности до ее границы. Затем, применяя циркуль, идентифицируем первую вершину точно на окружности. Аналогичным образом находим и определяем две оставшиеся вершины.
Полученные три вершины образуют треугольник внутри окружности, который можно отобразить на бумаге или создать 3D-модель. Этот метод построения треугольника является простым и эффективным, позволяя безошибочно определить вершины и получить правильную форму внутри окружности.
Метод трех параллельных линий

В данном разделе мы рассмотрим метод, основанный на использовании трех линий, которые параллельны друг другу. Этот метод представляет собой известную технику, которая широко используется в геометрии и позволяет находить треугольник, который можно вписать в окружность.
Для использования метода трех параллельных линий необходимо провести три линии, которые будут параллельны друг другу. Затем, используя циркуль и ранее отмеченные точки, необходимо создать окружность, которая будет описывать треугольник.
Этот метод является одним из самых простых и эффективных способов нахождения треугольника, вписанного в окружность. Он позволяет точно определить все три вершины треугольника, а также установить радиус окружности и ее центр. Это, в свою очередь, открывает широкие возможности для дальнейшего изучения данной фигуры и решения различных задач, связанных с ней.
Метод трех параллельных линий является важным инструментом при изучении треугольников и окружностей. Он предоставляет удобный и эффективный способ нахождения треугольника, который легко вписывается в окружность. Применение данного метода позволяет решать разнообразные геометрические задачи и анализировать свойства треугольников и окружностей.
Создание треугольника в окружности с использованием циркуля и перпендикуляра

Применение метода секущей и серединно-перпендикулярной для построения треугольника в окружности
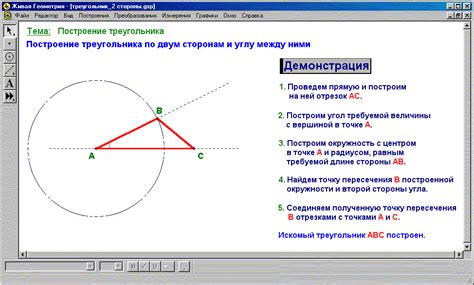
Метод секущей предлагает построение прямой линии через две вершины треугольника и точку на окружности, используя циркуль и линейку. Затем, при помощи метода серединно-перпендикулярной, определяется серединный перпендикуляр к данной прямой. Этот перпендикуляр пересекает окружность и представляет собой требуемую третью вершину треугольника.
| Метод секущей | Метод серединно-перпендикулярной |
| С использованием циркуля и линейки проводится прямая через две вершины треугольника и точку на окружности | По принципу равенства длин отрезков и угловых отношений, строится серединный перпендикуляр к прямой |
| Прямая пересекает окружность в двух точках | Серединный перпендикуляр пересекает окружность в точке, обозначающей третью вершину треугольника |
Таким образом, применение метода секущей и серединно-перпендикулярной позволяет точно определить положение вершин треугольника на окружности. Этот метод основан на совместном использовании геометрических принципов, которые позволяют эффективно проводить соответствующие построения с использованием циркуля. Он является одним из важных инструментов для работы с треугольниками в геометрии и строительстве.
Метод арка-сторона-сторона для построения треугольника в окружности

В данном разделе будет рассмотрен метод, основанный на использовании окружностей и сторон треугольника для его построения. Этот метод позволяет точно определить треугольник, вписанный в окружность, и вычислить координаты его вершин.
Вначале, используя циркуль, мы проводим две окружности, которые пересекаются в двух точках. Затем, с помощью линейки, проводим стороны треугольника, соединяющие эти точки. На этом этапе требуется аккуратность и точность, чтобы гарантировать правильность построения.
Далее, мы определяем координаты вершин треугольника, используя метод построения треугольника вписанным в окружность. А именно, для каждой вершины мы находим точку пересечения этой вершины с окружностью и записываем ее координаты. Таким образом, мы получаем точные координаты вершин треугольника.
- Шаг 1: Провести две окружности, используя циркуль
- Шаг 2: Провести стороны треугольника, используя линейку
- Шаг 3: Найти точки пересечения сторон с окружностями
- Шаг 4: Записать координаты вершин треугольника
Таким образом, метод арка-сторона-сторона позволяет нам создать треугольник в окружности, используя циркуль и линейку. Этот метод является надежным способом получить точные координаты вершин треугольника, что может быть полезно при решении различных геометрических задач.
Магия форм и линий: Волшебные способы создания фигур с помощью циркуля и точек пересечения медиан

Этот раздел посвящен захватывающему и уникальному миру использования циркуля и точек пересечения медиан для создания фигур, которые впечатляют своей элегантностью и симметрией. С помощью точечных инструментов и дополнительных манипуляций, мы сможем исследовать различные способы создания треугольника в окружности и понять их необычные свойства и возможности.
Одним из величайших достижений геометрии является умение создавать красивые и гармоничные фигуры с помощью циркуля и пересечения медиан. Мы рассмотрим, каким образом эти инструменты могут быть использованы, чтобы построить идеальный треугольник в окружности. Вместе с тем, мы узнаем о таинственных свойствах такого треугольника и его симметричной формы.
Используя точечные инструменты и исследуя разнообразные методы создания треугольника в окружности, можно обнаружить некоторые неожиданные законы природы и законы геометрии. Они позволят нам углубиться в мир линий и форм, расширить свои границы и открыть новые горизонты в геометрии.
В одном из методов, в точках пересечения медиан треугольника строятся специальные окружности. Используя эти окружности и возможности циркуля, мы можем создать треугольник, вписанный в окружность. Он будет обладать рядом удивительных свойств, например, равенством всех трех углов и равенством всех трех сторон.
Мастерство использования циркуля и точек пересечения медиан в создании треугольника в окружности является настоящим искусством. Оно требует не только понимания геометрических законов, но и чувства прекрасного, чтобы создать фигуру, которая отражает гармонию и совершенство геометрического мира.
Построение треугольника вокруг окружности с помощью радиусов и углов
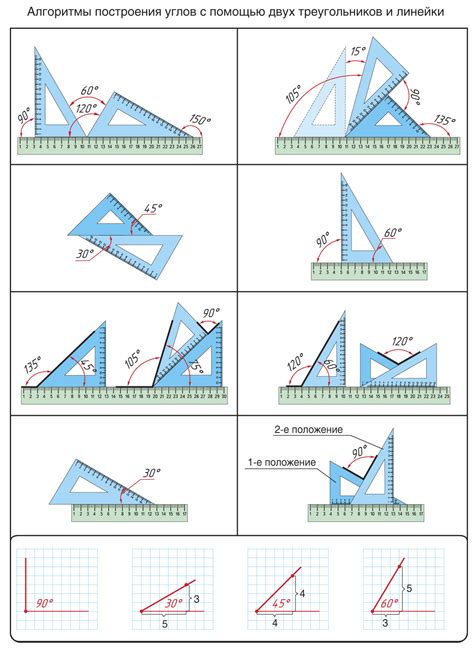
В данном разделе рассматривается метод построения треугольника, который описывает окружность, с использованием информации о радиусах и углах. При таком подходе исключается необходимость в прямолинейных линиях и циркулях, что делает процесс создания треугольника более удобным и интуитивно понятным.
При данном методе строительство треугольника начинается с окружности, чья граница представляет собой требуемый треугольник. Радиусы каждой из сторон треугольника измеряются и отмечаются на окружности, а соответствующие углы фиксируются с помощью измерительного инструмента. Затем, с использованием данной информации, треугольник постепенно прорисовывается путем соединения отмеченных точек.
Такой подход позволяет более свободно манипулировать размерами и формой треугольника, так как изменение радиусов и углов позволяет контролировать его геометрические параметры. Кроме того, использование радиусов и углов упрощает процесс построения треугольника и позволяет избежать сложных математических вычислений.
Метод построения треугольника в окружности с использованием радиусов и углов находит свое применение в различных областях, включая геометрическое моделирование, архитектуру и искусство. Он представляет собой удобный инструмент, который позволяет создавать простые и сложные треугольники с высокой точностью и эстетической гармонией.
Вопрос-ответ

Можно ли построить треугольник в окружности, используя только циркуль?
Да, построить треугольник в окружности с использованием только циркуля возможно. Для этого необходимо провести две окружности, которые пересекаются в двух точках. Соединив эти точки и центр окружностей, получим треугольник внутри окружности.
Как использовать циркуль для создания треугольника в окружности?
Для создания треугольника в окружности с использованием циркуля, нужно выбрать центр будущей окружности и выбрать радиус. Затем, с одного конца радиуса провести окружность, а с другого конца радиуса провести еще одну окружность. Точки пересечения окружностей и центр окружностей образуют треугольник в окружности.
Какие еще методы с использованием циркуля можно использовать для создания треугольника в окружности?
Помимо метода с проведением двух окружностей, использующихся для построения треугольника в окружности, можно также использовать метод проведения биссектрисы от двух различных дуг окружности. Биссектрисы пересекаются в вершине треугольника, а середины этих дуг являются точками, лежащими на окружности.



