Математика – это стройная и точная наука, которая позволяет нам исследовать и понимать мир вокруг нас с помощью чисел, формул и выражений. Однако, иногда нам предстоит столкнуться с комплексными выражениями, где требуется найти значение с использованием переменных. Одним из таких выражений является 5x 15y 1.
Итак, давайте попробуем разобраться, что означает это выражение. Здесь мы имеем две переменные: x и y, которые представляют неизвестные значения. Окруженный числами 5 и 1, это выражение демонстрирует, что переменные множатся и складываются друг с другом. Однако, что же будет являться конечным результатом?
Чтобы узнать значение выражения 5x 15y 1, нам необходимо знать, какие значения присвоены переменным x и y. Если мы знаем конкретные значения для каждой переменной, можем подставить их в выражение и произвести несложные математические операции для нахождения окончательного ответа. Однако, без таких значений, решение задачи становится сложнее.
Понимание базовых математических операций
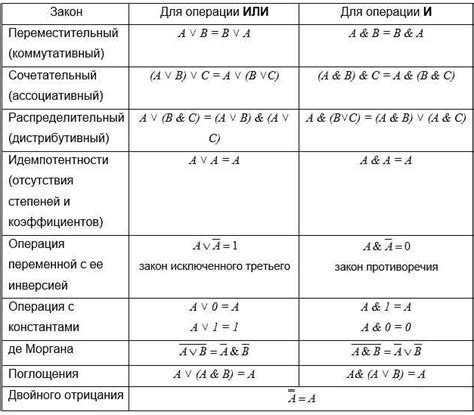
Сложение - это операция, при которой два или более числа объединяются в одно число, называемое суммой. Сумму двух чисел можно вычислить, складывая их значения.
Вычитание - это операция, при которой одно число вычитается из другого. Вычитание позволяет найти разницу между двумя значениями.
Умножение - это операция, при которой одно число увеличивается в несколько раз, когда оно умножается на другое число, называемое множителем.
Деление - это операция, обратная умножению. Она позволяет разделить одно число на другое и найти результат этого разделения, называемый частным.
Использование и понимание базовых математических операций является основой для решения различных задач и проблем в нашей повседневной жизни, а также в научных и технических областях. Умение выполнять эти операции с числами дает нам возможность анализировать и интерпретировать данные, решать уравнения и задачи, а также строить логические и математические модели.
Описание выражения

В математике существует понятие выражения, которое представляет собой набор математических символов, чисел и операций, объединенных в определенной последовательности. Выражение может состоять из переменных, чисел и знаков операций, таких как сложение, вычитание, умножение и деление.
Выражение может быть использовано для вычисления значения или для представления математической формулы. Оно может содержать одну или несколько переменных, которые заменяются на конкретные числа или значения в рамках заданного контекста.
Когда рассматривается выражение в контексте его значения, важно понимать, что оно может иметь разные результаты в зависимости от значений переменных. Таким образом, выражение является гибким инструментом, который может быть использован для моделирования и анализа различных математических задач или явлений.
| Примеры выражений: |
| 2 + 3 |
| 4 * x |
| y^2 - 7 |
Математическое значение алгебраического выражения

Одним из примеров алгебраического выражения является данное нам выражение "5x 15y 1". Здесь "5x", "15y" и "1" представляют собой части выражения, каждая из которых имеет свое значение. В данном случае, "5x" и "15y" обозначают произведение числа на переменную, а "1" - отдельную числовую составляющую. Нашей задачей является вычислить значение данного выражения.
Для решения данной задачи необходимо знать значения переменных x и y. Подставив эти значения в выражение и выполнить соответствующие арифметические операции, мы сможем найти значение всего выражения.
Важно понимать, что значение выражения может быть числом, как в данном случае, или другим математическим объектом, таким как вектор или матрица. В зависимости от задачи, значения выражения могут быть интерпретированы по-разному и использованы для дальнейших расчетов или анализа.
Работа с переменными в алгебраических выражениях
Как определить значения переменных в математическом выражении?
1. Использование системы уравнений: одним из способов определить значения переменных в выражении является построение системы уравнений. В этом случае переменные обозначаются буквами, и мы можем составить систему уравнений, основываясь на условиях задачи. Решение системы позволит нам найти значения переменных.
2. Подстановка значений: другим способом определить значения переменных является пошаговая подстановка значений в выражение и вычисление результата. Путем итераций мы можем найти значения, при которых выражение принимает заданное значение. Подстановка может использоваться как самостоятельный метод, так и в сочетании с другими методами.
При определении значений переменных в выражении важно учитывать контекст проблемы и условия, которые могут ограничивать возможные значения переменных. Также можно использовать дополнительные методы, такие как графическое представление и численное моделирование, для подтверждения полученных результатов.
Операции с переменными в арифметических выражениях

В данном разделе рассмотрим основные операции, которые можно выполнять с переменными в арифметических выражениях. При выполнении математических операций с переменными важно разбираться в их смысле и правилах применения, чтобы получить правильный результат.
Переменные в арифметических выражениях позволяют задавать значения, которые могут изменяться. Они являются неизвестными, которые нужно найти или использовать для выполнения математических операций.
В выражении 5x 15y 1, переменные x и y могут представлять различные значения. Операции с этими переменными можно выполнять с использованием различных математических операторов, таких как сложение, вычитание, умножение и деление.
Результат выражения 5x 15y 1 будет зависеть от значений переменных x и y. Путем замены переменных на конкретные значения и выполнения операций можно получить конечный результат, который можно интерпретировать и использовать в дальнейших вычислениях или анализе данных.
Вычисление суммы числового выражения с переменными коэффициентами

Для вычисления значения выражения 5x + 15y + 1 необходимо знать конкретные значения переменных x и y. При заданных значениях переменных можно приступить к расчету. В выражении 5x + 15y + 1 каждое слагаемое представляет из себя произведение коэффициента на значение переменной. Значения переменных можно выбрать произвольно, в зависимости от поставленной задачи или условий задачи, в которых дано значение выражения.
Пример расчета данного выражения:
- Пусть значение переменной x равно 2, а значение переменной y равно 3.
- Подставляем эти значения в выражение: 5*2 + 15*3 + 1.
- Выполняем умножения: 10 + 45 + 1.
- Складываем полученные произведения: 56.
Таким образом, при значениях x = 2 и y = 3, значение выражения 5x + 15y + 1 составляет 56.
Что подразумевается данным математическим выражением?

При анализе выражения 5x 15y 1, возникает вопрос о том, какое значение оно имеет и что означает для нас.
- Выражение включает переменные и числа, которые могут взаимодействовать друг с другом.
- Коэффициенты перед переменными, такие как 5 и 15, могут указывать на важность и вклад каждой переменной в итоговое значение.
- Буквы x и y представляют неизвестные значения и могут иметь различные значения в разных ситуациях.
- Число 1 может быть некоторой константой, которая дополняет выражение и определяет его базовое значение.
Изучение и понимание данного выражения позволяет проникнуть в сущность математических формул и их применение в решении практических задач.
Как найти результат вычисления для заданных значений переменных?
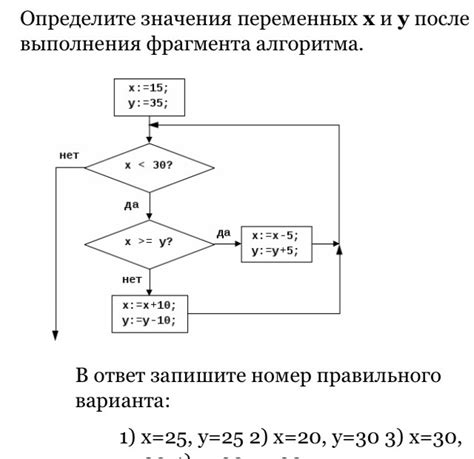
В данном разделе мы рассмотрим методы и правила для определения значения выражения, если заданы конкретные значения переменных x и y. Подробно разберем процесс вычисления, используя различные операции и приемы математики.
- Шаг 1: Замена переменных
- Шаг 2: Выполнение операций
- Шаг 3: Упрощение выражения
- Шаг 4: Получение результата
Первым шагом в нахождении результата вычисления выражения для заданных значений x и y будет замена переменных на эти значения. Для этого подставим указанные значения вместо соответствующих переменных в выражении.
После замены переменных на конкретные значения, следующим шагом будет выполнение операций в выражении. Произведем умножение, сложение, вычитание и деление в указанном порядке, чтобы получить итоговый результат.
В некоторых случаях выражение может быть упрощено путем сокращения или объединения частей. Если есть возможность упростить выражение, то это должно быть сделано перед окончательным вычислением.
После выполнения всех предыдущих шагов, мы получим окончательное значение выражения для заданных значений переменных x и y. Это будет численный результат, который можно использовать для дальнейших вычислений или анализа.
Теперь, когда мы познакомились с общими принципами поиска значения выражения для конкретных значений x и y, перейдем к более детальному изучению каждого из шагов.
Примеры вычисления значения алгебраических выражений с переменными

Рассмотрим, например, выражение 5x, где переменная x может принимать различные значения. Чтобы узнать значение данного выражения для конкретного числа x, нужно умножить значение переменной на 5.
- Пример 1:
- Пример 2:
- Пример 3:
Пусть x = 2. Тогда значение выражения 5x будет равно 5 * 2 = 10.
Если x = -3, то значение выражения 5x будет равно 5 * -3 = -15.
При x = 0, значение выражения 5x будет равно 5 * 0 = 0.
Таким образом, значения выражения 5x зависят от значения переменной x и вычисляются путем умножения этого значения на 5.
Практическое использование линейного выражения 5x + 15y + 1

Линейные выражения, как 5x + 15y + 1, находят широкое применение в решении реальных задач различных областей. Эти выражения позволяют учитывать взаимосвязи между различными переменными и использовать их для расчетов и предсказаний.
Финансовая аналитика: Линейные выражения могут быть использованы для моделирования и анализа финансовых данных. Например, можно использовать 5x для представления общих переменных, таких как количество проданных товаров, и 15y для представления переменной, такой как стоимость единицы товара. Выражение 5x + 15y + 1 может использоваться для предсказания общей стоимости продажи при заданных значениях x и y.
Инженерия: Линейные выражения также могут быть применены в инженерии для описания физических величин и решения инженерных задач. Например, 5x может представлять расстояние, а 15y - время. Тогда выражение 5x + 15y + 1 может использоваться для вычисления общего времени и расстояния в задачах связанных с движением.
Таким образом, линейное выражение 5x + 15y + 1 имеет практическое применение в различных областях и может быть использовано для решения разнообразных задач, предсказания и анализа данных.
Понятие линейной комбинации

Линейная комбинация представляет собой сумму или разность чисел, умноженных на некоторые коэффициенты. В нашем случае, заданное выражение 5x + 15y + 1 можно рассматривать как линейную комбинацию переменных x и y, где каждое число умножается на коэффициент.
Понимание понятия линейной комбинации позволяет нам работать с линейными уравнениями, системами уравнений, векторами и многими другими математическими объектами. Это понятие является основой для дальнейшего изучения алгебры и линейной алгебры в частности.
Вопрос-ответ

Как найти значение выражения 5x 15y 1?
Для нахождения значения этого выражения нужно подставить конкретные значения переменных x и y и выполнить операции. Например, если x = 2 и y = 3, то выражение будет выглядеть так: 5 * 2 + 15 * 3 + 1 = 10 + 45 + 1 = 56.
Что означает символ "x" в выражении 5x 15y 1?
В данном контексте символ "x" является переменной, которая может принимать различные значения. Она используется для обозначения неизвестного числа или величины. В данном выражении она умножается на 5.
В каком порядке выполняются операции в выражении 5x 15y 1?
В данном выражении выполняется умножение и сложение. Сначала умножаются значения переменных x и y на соответствующие коэффициенты: 5x и 15y. Затем результаты умножения складываются с единицей: 5x + 15y + 1.
Можно ли упростить выражение 5x 15y 1?
Да, выражение 5x 15y 1 можно упростить, если известны конкретные значения переменных x и y. Для этого нужно выполнить умножение и сложение. Например, если x = 2 и y = 3, то выражение можно упростить так: 5 * 2 + 15 * 3 + 1 = 10 + 45 + 1 = 56.
Какие значения переменных x и y подставить, чтобы получить максимальный результат выражения 5x 15y 1?
Для нахождения максимального значения выражения 5x 15y 1 нужно выбрать такие значения переменных x и y, которые максимизируют результат умножения и сложения. Например, можно подставить x = 10 и y = 5, тогда выражение будет выглядеть так: 5 * 10 + 15 * 5 + 1 = 50 + 75 + 1 = 126.
Как найти значение выражения 5x 15y 1?
Для того чтобы найти значение выражения 5x 15y 1, необходимо знать значения переменных x и y. Подставьте значения переменных вместо x и y в данное выражение и выполните соответствующие математические операции. Например, если x = 2 и y = 3, то 5x 15y 1 будет равно 5*2 + 15*3 + 1 = 10 + 45 + 1 = 56.



