Когда мы решаем математические задачи, часто сталкиваемся с геометрическими фигурами, в том числе и с трапецией. Одним из ключевых понятий, связанных с этой фигурой, является высота, которая играет важную роль при расчетах ее площади и других геометрических параметров. Но как найти эту высоту и какие формулы применять для ее расчета?
Высота равнобедренной трапеции является перпендикуляром, опущенным из одного основания на противоположное основание. Она является важным элементом для нахождения площади трапеции и других ее характеристик. Для ее вычисления существует специальная формула, которую мы рассмотрим ниже.
Чтобы найти высоту равнобедренной трапеции, можно воспользоваться теоремой Пифагора. Зная длины оснований и бокового ребра, можно вычислить длину высоты, применяя данную формулу. Такой подход позволяет нам более точно определить высоту и использовать ее для решения задач различной сложности.
Особенности равнобедренной трапеции

Первая особенность равнобедренной трапеции заключается в том, что ее основания равны по длине. Это означает, что противоположные стороны параллельны и имеют одинаковую длину. Такая симметрия делает равнобедренную трапецию эстетически привлекательной и удобной для работы с ней.
Вторая особенность равнобедренной трапеции связана с углами. Внутренние углы, образованные основаниями и боковыми сторонами, равны между собой. Это означает, что две диагонали равнобедренной трапеции делятся пополам и образуют одинаковые углы с основаниями.
Третья особенность связана с диагоналями равнобедренной трапеции. Замечательное свойство равнобедренной трапеции заключается в том, что ее диагонали перпендикулярны. Это значит, что они встречаются под прямым углом и делятся пополам. Это свойство позволяет использовать диагонали для нахождения высоты равнобедренной трапеции.
Определение равнобедренной трапеции

Равнобедренная трапеция – это трапеция, у которой две некратные основания равны по длине. В дополнение к этому, равнобедренная трапеция также имеет два равных угла при основаниях. Это значит, что две некратные боковые стороны равны между собой, в то время как другие две стороны некратны, но также параллельны.
Если мы обратим внимание на геометрическую форму равнобедренной трапеции, то можем заметить, что один из ее углов является прямым. Это происходит потому, что сумма углов трапеции всегда равна 360 градусов, а два равных при основаниях угла в сумме дают 180 градусов. Этот факт делает равнобедренную трапецию более удобной для решения геометрических задач.
Определение равнобедренной трапеции может быть полезно при изучении ее свойств и применении ее в различных математических и геометрических задачах. Понимание конструкции, углов и сторон равнобедренной трапеции поможет в дальнейшем решении задач, требующих вычисления площади и координатных точек.
Особенности фигуры с равными сторонами и одинаковыми углами

В этом разделе мы рассмотрим особенности фигуры, которая имеет две равные стороны и два одинаковых угла. Такая фигура называется равнобедренной трапецией. Различные свойства и характеристики этой фигуры позволяют нам более глубоко понять ее структуру и использование в различных геометрических задачах.
Одним из ключевых свойств равнобедренной трапеции является симметричность относительно ее базы - линии, соединяющей основания фигуры. Это означает, что мы можем провести одну или несколько осей симметрии, которые разделят трапецию на две одинаковые части. Эта особенность позволяет нам использовать равнобедренную трапецию в конструкциях, где требуется равномерное распределение нагрузки или симметрия.
Еще одной интересной особенностью равнобедренной трапеции является возможность использования пропорциональности ее сторон. Так, если мы знаем длины оснований трапеции и одну из ее высот, то можем легко определить длину другой высоты. Это свойство позволяет нам проводить различные вычисления и строить соотношения между размерами фигуры.
- Симметричность относительно базы
- Пропорциональность сторон
Таким образом, равнобедренная трапеция представляет собой геометрическую фигуру с рядом уникальных свойств и особенностей. Изучение и понимание этих характеристик помогают нам использовать трапецию в различных задачах, связанных с геометрией и пространственным моделированием.
Как определить высоту равнобедренной трапеции?
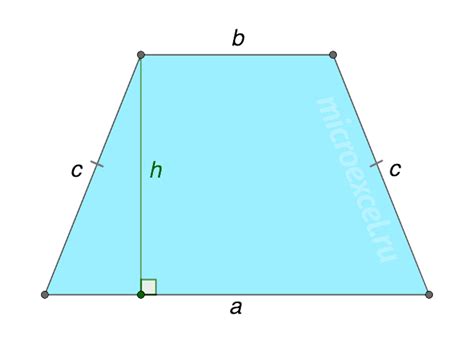
Один из методов нахождения высоты равнобедренной трапеции заключается в использовании отношения боковой стороны и основания.
Если вам известна боковая сторона и длина основания, вы можете использовать эту формулу для нахождения высоты:
Высота = (Боковая сторона * 2) / (Разность оснований)
Данная формула поможет вам определить, какая высота необходима для равнобедренной трапеции с заданными параметрами. При использовании данного метода не забывайте учесть, что боковая сторона должна быть параллельна основаниям трапеции.
Определение основных характеристик равнобедренной трапеции

Одной из основных характеристик равнобедренной трапеции является ее основание. В данном случае основание представляет собой длинную сторону фигуры, по которой она устанавливается на плоскость. Помимо этого, трапеция также имеет два боковых ребра, которые соединяют основание и вершины, называемые равными бедрами. Как следует из названия, эти два боковых ребра равны между собой, что делает данную фигуру симметричной.
Другой важной характеристикой равнобедренной трапеции является ее высота. Высота относится к линейному измерению фигуры и определяется как перпендикулярная проведенная от основания до противоположной стороны, образованной боковыми ребрами. Высота способна разделить фигуру на два равных треугольника, что является одним из ключевых свойств равнобедренной трапеции.
Использование математической формулы для определения вертикального отрезка в равнобедренной геометрической фигуре

В данном разделе рассмотрим методический подход к определению размера отрезка, который находится перпендикулярно к основанию равнобедренной геометрической фигуры. Отрезок, полученный с использованием вычислений по специальной формуле, позволяет эффективно определить требуемую вертикальную высоту нашей фигуры, исключая необходимость в дополнительных измерениях или сложных методах.
Перед приступлением к использованию формулы, необходимо убедиться в правильном определении оснований фигуры, которые считаются равными по длине. Формула включает в себя значения основания и угла между ними, и через соответствующие математические операции возможно быстрое и точное определение требуемой высоты фигуры. Важно отметить, что использование данной формулы предполагает тщательное следование инструкциям и математическим правилам, чтобы не допустить ошибок в расчетах и получить достоверные результаты.
- Шаг 1: Задать значения основания фигуры и угла между ними.
- Шаг 2: Перейти к формуле расчета высоты и внести известные данные.
- Шаг 3: Произвести необходимые вычисления с использованием математических операций.
- Шаг 4: Получить окончательное значение вертикальной высоты фигуры.
Использование данного метода позволяет точно и быстро определить значение требуемого вертикального отрезка в равнобедренной геометрической фигуре. Правильное применение формулы гарантирует достоверность и точность результатов, позволяя легко выполнять расчеты без необходимости в сложных и длительных измерениях.
Вопрос-ответ

Какая формула позволяет рассчитать высоту равнобедренной трапеции?
Формула для расчета высоты равнобедренной трапеции имеет следующий вид: h = √(b^2 - (a^2/4)), где h - высота, b - длина основания трапеции, a - длина одного из боковых сторон.
Каким образом можно определить длину основания равнобедренной трапеции, если известна только ее высота и длина одной из боковых сторон?
Длину основания равнобедренной трапеции можно определить по следующей формуле: b = √(h^2 + (a^2/4)), где b - длина основания, h - высота, a - длина одного из боковых сторон.
Какая геометрическая интерпретация у формулы расчета высоты равнобедренной трапеции?
Геометрически формула для расчета высоты равнобедренной трапеции означает, что высота является биссектрисой угла основания трапеции и делит его на два равных отрезка, а также является катетом прямоугольного треугольника, который образуется между высотой и половиной основания.
Можно ли расчитать высоту равнобедренной трапеции, зная только длины основания и другой стороны, не являющейся боковой?
Да, это возможно. Если известны длина основания (b) и другая сторона t, не являющаяся боковой, высоту трапеции можно расчитать по формуле: h = (2bt)/(b + 2t).



