Геометрия, как одна из основных разделов математики, изучает пространственные и фигурные отношения, а также их свойства. Понимание природы и поведения точек в геометрии является важным аспектом, который позволяет анализировать и доказывать различные утверждения и теоремы. В данной статье мы сосредоточимся на изучении произвольности точек, исследуя их способность занимать любые положения в пространстве.
Изучение произвольности точек имеет широкий спектр применений в геометрии, начиная от анализа сложных трехмерных фигур и пространственных конструкций до решения задач локализации и навигации в реальном мире. Понимание свойств произвольных точек позволяет нам анализировать геометрические отношения и построения, а также применять их в различных областях науки и техники.
Роль уникальных точек в мире математики

В данном разделе рассматривается значимость определённых мест на плоскости, которые играют важную роль в математических теориях и концепциях. Эти особые точки, которые мы обозначим как abcd, оказывают значительное влияние на различные области математики и их рассмотрение основано на их произвольности.
Необходимо отметить, что abcd не являются случайно выбранными точками, а скорее представляют собой точки, которые обладают определёнными характеристиками и свойствами в зависимости от контекста и задачи. Понимание и изучение этих точек позволяет рассмотреть математические конструкции более глубоко и полно.
В одном аспекте abcd может означать четыре пересекающиеся прямые, которые образуют основу для решения геометрических задач и разработки специфических методов анализа. Однако эти точки могут также рассматриваться в контексте системы координат, играя роль координатных осей и позволяя определить положение и направление в пространстве.
Помимо этого, abcd могут взаимодействовать в алгебраическом смысле, выступая в качестве переменных или неизвестных, которые подлежат анализу и исследованию для решения уравнений и систем. В этих ситуациях abcd обеспечивают гибкость и разнообразие методов в мировой математике.
Исследование роли abcd в таких разнообразных областях математики позволяет углубить понимание и рассмотреть их переграничную значимость. При этом каждая из этих точек имеет свою уникальность и вносит свой собственный вклад в общую картину математического знания и решения задач.
Непреходящая ценность образов точек abcd в геометрии
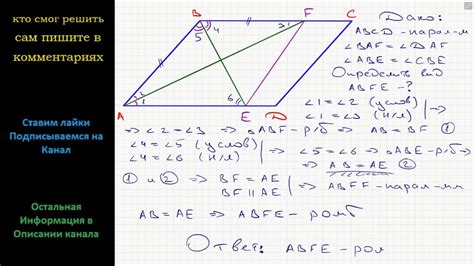
В геометрии существуют особые точки, которые играют важную роль в построении и анализе фигур, а именно точки abcd. В данном разделе мы раскроем их значимость и покажем, как они влияют на структуру и свойства геометрических объектов.
Каждая из точек abcd обладает своей уникальной характеристикой и способностью влиять на понимание и изучение геометрии. Используя эти точки, мы можем строить различные фигуры, определять их свойства, вычислять площади и периметры. Все это делает точки abcd незаменимыми инструментами для создания и анализа сложных геометрических конструкций.
Отметим, что точки abcd являются произвольными, что обеспечивает гибкость и свободу в создании фигур. Вместе они позволяют нам визуализировать абстрактные понятия и демонстрировать свойства математических объектов. Как заметим, значение этих точек расширяется по мере углубления в геометрии, их применение выходит за рамки простых построений и переходит к решению сложных задач и доказательств теорем.
Свойства и применение особых точек в математическом изучении системы abcd
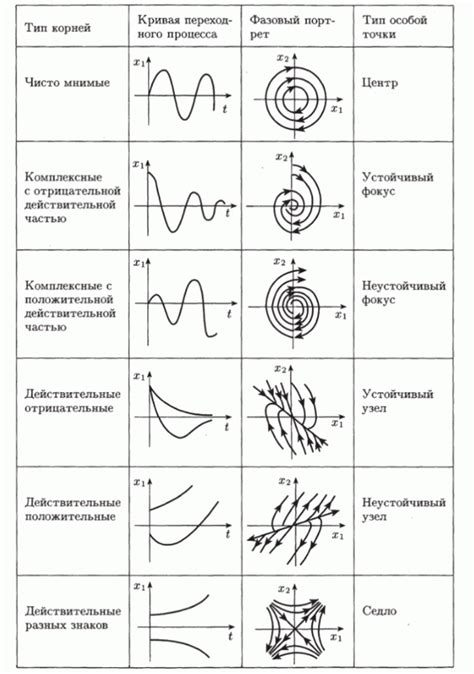
В данном разделе рассматриваются особые свойства и возможные применения точек системы abcd, обладающих уникальными характеристиками.
Эти точки, избранные из произвольных величин, имеют особую роль в математических рассуждениях, позволяя углубить понимание и применение данной системы.
1. Ключевые свойства точек:
В рамках данного раздела будут представлены уникальные характеристики точек системы abcd.
Будет рассмотрена их функциональность и зависимость от других элементов данной системы.
Также будет обращено внимание на соединения, пересечения и отношения между этими точками, что откроет новые возможности для дальнейших исследований.
2. Практическое применение точек:
В этой части статьи будет обсуждаться практическое применение особых точек системы abcd в реальных задачах.
Приведены конкретные примеры иллюстрирующие использование этих точек в различных областях науки и техники.
Уделено внимание актуальности применения и значимости полученных результатов для развития математики и других научных дисциплин.
В итоге изучение свойств и применение точек системы abcd не только расширяют теоретические знания о данной системе, но также позволяют использовать их в практических задачах, повышая применимость математики в реальном мире.
Универсальная расторопность и её подтверждение

В мире математики существует захватывающая область, где точки рассеяны по пространству с невиданной произвольностью. Какой же секрет кроется за их расположением и возможностью выбора? На этот вопрос мы попытаемся найти ответ в данном разделе, не углубляясь в конкретные термины и определения.
Речь пойдет о теории, которая раскрывает суть искусства выбора точек в математическом пространстве. Она показывает, что точки несущие в себе свободу решений, являются главным строительным элементом различных математических систем. Именно эти точки, будучи разбросанными вокруг нас, формируют кратчайшие пути, идеальные графики и примеры максимальной оптимизации.
Приготовьтесь к погружению в захватывающий мир произвольности и откройте для себя загадочные законы, управляющие расстановкой точек в математическом пространстве. Вперед, к новым горизонтам познания, где нет места для ограничений и предсказуемости!
Методы подтверждения взаимной независимости точек abcd в математических рассуждениях

1. Сравнение координат: Один из методов подтверждения произвольности точек abcd заключается в анализе их координат. Путем сравнения значений координат по различным осям, можно убедиться, что данные точки не обладают явными закономерностями или зависимостями, что подтверждает их произвольность. На основе этого наблюдения мы можем строить дальнейшие математические рассуждения.
2. Использование свойств фигур: Другим полезным методом является анализ свойств геометрических фигур, в которых расположены точки abcd. Исследуя углы, стороны, диагонали и другие характеристики фигур, мы можем показать, что выбор этих точек не связан с какими-либо предопределенными условиями или ограничениями. Таким образом, мы можем утверждать, что точки abcd могут быть размещены произвольным образом в рамках изучаемых геометрических структур.
Таким образом, используя разнообразные методы анализа, мы можем подтвердить, что выбор точек abcd в математических доказательствах не является случайным, а основан на строгой математической логике и рассуждениях.
Анализ аргументов о произвольности расположения точек в различных математических теориях

В данном разделе мы рассмотрим различные подходы и теории, в которых освещается вопрос о возможности свободного выбора расположения точек. Мы изучим разнообразные рассуждения, которые позволяют нам утверждать о произвольности точек в разных областях математической науки.
Далее мы обратимся к фундаментальным теориям, где произвольность точек может быть связана с понятием мощности различных множеств. Мы рассмотрим, как свободный выбор расположения абстрактных точек может быть оправдан и отражен в структуре теоретических конструкций.
Наш анализ также включит рассмотрение практических примеров, где произвольность точек играет важную роль. Мы разберем такие области математики, как геометрия, топология, анализ, исследуя способы применения произвольных точек и связанных с ними теоретических концепций.
Итак, в этом разделе мы углубимся в изучение различных математических теорий и их подходов к доказательству произвольности точек, что поможет нам лучше понять разнообразие аргументов, связанных с этим важным понятием в научном исследовании.
Практическое применение случайных точек столетиями в математических задачах

Благодаря этой технике, мы можем гибко анализировать различные математические модели и проблемы, исследуя их на основе случайно выбранных точек. Применение произвольности разными способами позволяет нам оценивать вероятности, проводить статистический анализ данных, создавать новые гипотезы и проверять их на достоверность.
Техника использования случайных точек широко применяется в проблемах оптимизации, численных методах, графическом моделировании и других областях математики. Путем выбора различных произвольных точек, мы можем исследовать функциональные зависимости, находить оптимальные значения и решать сложные оптимизационные задачи с высокой степенью надежности и точности.
Однако, важно отметить, что использование случайных точек требует тщательной проверки результатов и анализа, чтобы избежать возможных ошибок и искажений. Несмотря на свою случайность и произвольность, точки должны быть подвергнуты математической обработке и статистической проверке, чтобы их использование в задачах было корректным и достоверным.
Вопрос-ответ

Как доказывается произвольность точек abcd в математике?
Доказательство произвольности точек abcd в математике основывается на принципе некоторого множества аксиом или теорем, которые определяют свойства и отношения точек в геометрии. Например, если точки abcd образуют четырехугольник, то с использованием аналитической геометрии и геометрических доказательств можно установить независимость между ними и отсутствие особых свойств, которые объединяют их в определенную геометрическую фигуру.
Какие примеры можно привести для доказательства произвольности точек abcd?
Примером доказательства произвольности могут служить простейшие геометрические фигуры, такие как равносторонний треугольник, квадрат, ромб и т.д. В этих случаях, используя определения и свойства данных фигур, можно показать, что точки a, b, c и d не имеют никаких специфических связей между собой, и их положение может быть произвольным и независимым.
Какая роль играет аналитическая геометрия в доказательстве произвольности точек abcd?
Аналитическая геометрия является одним из методов, которые можно использовать для доказательства произвольности точек abcd в математике. С помощью аналитической геометрии можно представить координаты точек a, b, c и d в системе координат, а затем использовать геометрические методы и свойства для доказательства их произвольности. Таким образом, аналитическая геометрия позволяет установить независимость и произвольность данных точек в геометрическом пространстве.



