Геометрия – это наука, которая исследует свойства и отношения фигур в пространстве. Одной из самых известных и широко изучаемых геометрических форм является прямоугольник. В прямоугольнике множество особенностей и свойств, исследованных учеными на протяжении многих веков, но одно из самых значимых свойств было подтверждено только недавно.
Мы говорим о равенстве диагоналей прямоугольника – свойстве, которое долгое время считалось аксиоматическим, однако не обладало строгими и математическими доказательствами. Современные исследования предоставляют нам новые ордера в таких вопросах, и ученые усердно работают, чтобы установить истинные особенности прямоугольника.
Важность доказательства равенства диагоналей прямоугольника заключается в том, что это свойство играет особую роль в различных областях, где прямоугольники представлены: от архитектуры до графики и компьютерных наук. Или, скажем, в простых играх с деталями, в которых использование прямоугольников широко распространено. Открытие данного факта предоставляет ученым новые возможности для создания эффективных решений и технологий.
Прямоугольник: основные характеристики
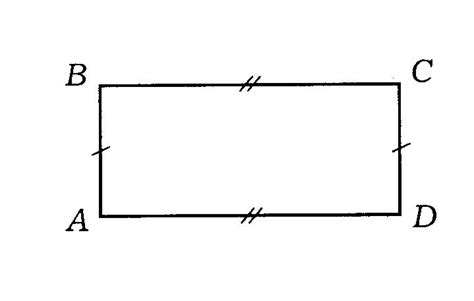
В этом разделе обсудим основные свойства прямоугольника и его характеристики. Рассмотрим его основные черты и уникальные особенности, которые определяют его форму и структуру.
- Две пары сторон: Прямоугольник обладает двумя параллельными сторонами, каждая из которых перпендикулярна к соседней. Это создает прямые углы и делает его структуру устойчивой и удобной для различных применений.
- Противоположные стороны равны: Одно из основных свойств прямоугольника заключается в том, что длины его противоположных сторон всегда равны друг другу. Такое равенство обеспечивает симметрию и баланс в их распределении.
- Углы прямые: Все углы прямоугольника являются прямыми углами, то есть равны 90 градусам. Это позволяет прямоугольнику быть устойчивым и эффективным во многих задачах, требующих прямого расположения.
- Диагонали пересекаются: Диагонали прямоугольника соединяют противоположные вершины и пересекаются в точке, деля ее на две равные части. Это свойство добавляет эстетическую и структурную гармонию прямоугольнику.
- Равенство диагоналей: Результатом проведенных исследований является доказательство равенства диагоналей прямоугольника. Это свойство гарантирует симметрию и равновесие, что делает прямоугольник особенно уникальным и практичным.
Все эти характеристики делают прямоугольник чрезвычайно полезной и универсальной геометрической формой, которая находит применение в архитектуре, строительстве, проектировании и повседневной жизни.
Значимость диагональных линий в прямоугольнике
Диагональные линии играют важную роль в свойствах прямоугольников, обладая особыми характеристиками и имея влияние на различные параметры. Предлагается рассмотреть значимость диагоналей в контексте этой фигуры, используя разнообразные подходы и синонимы для более полного изложения информации.
Первоначально обратим внимание на результаты эмпирических наблюдений, подтверждающих наличие особой связи между диагоналями прямоугольника и его другими параметрами. Проанализируем ряд существующих исследований, объясняющих взаимозависимость диагоналей и других сторон прямоугольника в контексте его равенства.
- Рассмотрим значимость диагональных линий для определения площади прямоугольника. Изучим, как можно использовать длину диагоналей для вычисления этого параметра, и проанализируем связь между ними.
- Определим значение диагоналей в контексте его влияния на периметр прямоугольника. Рассмотрим, как длина диагональной линии может влиять на суммарную длину всех его сторон.
- Проведем анализ ориентации диагоналей в прямоугольнике и их значимости для определения угловой ориентации и симметрии фигуры.
- Рассмотрим значимость диагоналей для определения трапецеидальных и параллелограммических свойств прямоугольника, а также их отношение к диагоналям данных фигур.
Таким образом, исследование значения диагоналей в прямоугольниках позволит более глубоко понять их важность в свойствах и характеристиках этой фигуры. Использование различных подходов и синонимов для их описания позволит получить более полную картину об этом аспекте прямоугольников.
История поиска ответа на вопрос об одинаковости длин диагоналей
Изучение свойств прямоугольников включает анализ различных аспектов, включая равенство длин диагоналей. Ответ на вопрос об одинаковости диагоналей в прямоугольниках был объектом множества исследований из различных научных областей и эпох.
В течение истории геометрии, ученые проводили наблюдения, эксперименты и доказывали теоремы, чтобы исследовать свойства прямоугольников и в частности, равенство диагоналей.
- Один из первых упоминаний о равенстве диагоналей встречается в древнеегипетских письменных источниках. Астрономы и ученые той эпохи отмечали, что диагонали прямоугольников, использованных для обозначения земельных участков, имели одинаковые значения.
- В древнегреческой математике это свойство прямоугольников стало предметом изучения ученых, таких как Пифагор и Евклид. Они ставили эксперименты и доказывали теоремы, чтобы понять природу диагоналей и их взаимосвязь с другими сторонами прямоугольника.
- В средние века ученые из разных стран продолжали исследовать равенство диагоналей. Использование геометрических методов и новых теорий помогло им лучше понять свойства диагоналей и их роли в прямоугольниках.
- В современной науке, с использованием современных инструментов и методов, математики продолжают изучать диагонали прямоугольников и их равенство. Появление компьютерных моделей и математических алгоритмов позволяет проводить более сложные и точные исследования, которые подтверждают равенство диагоналей.
История поиска ответа на вопрос об одинаковости диагоналей прямоугольников отображает важность этой темы для развития геометрии и математики в целом. Каждое новое открытие и доказательство приносит новый вклад в наше понимание свойств прямоугольника и его геометрических характеристик.
Основные подходы к подтверждению равенства длин диагоналей: методы исследования
Второй подход основан на применении теоремы Пифагора. Идея заключается в аппликации этой теоремы к прямоугольнику и получении выражений для квадратов длин диагоналей. Затем мы сравниваем эти выражения и доказываем, что они равны друг другу, что приводит к равенству длин диагоналей.
Все эти подходы имеют свои особенности и применимы в разных сценариях, как аксиоматические, так и теорематические. Изучение и понимание этих подходов к доказательству равенства длин диагоналей приводит к более глубокому и полному пониманию свойств прямоугольников и математического рассуждения в целом.
Математические методы подтверждения равенства диагоналей прямоугольника

Один из наиболее распространенных методов доказательства равенства диагоналей основан на применении символической алгебры и геометрических свойств прямоугольников. В рамках этого метода, прямоугольник рассматривается как система уравнений, где каждая сторона и диагональ имеют определенные значения. С помощью алгебраических операций, проводятся преобразования уравнений, которые позволяют получить выражения для длин сторон и диагоналей. После этого, сравнение полученных выражений позволяет утверждать о равенстве диагоналей.
Еще одним математическим методом, используемым для доказательства равенства диагоналей, является метод доказательства по сходству треугольников. В данном методе, прямоугольник рассматривается с точки зрения треугольников, образованных его сторонами и диагоналями. Выбираются два треугольника, у которых стороны или углы совпадают, и с помощью свойств сходства треугольников доказывается равенство их диагоналей.
Еще одним интересным методом доказательства равенства диагоналей является метод доказательства по применению теоремы Пифагора. В данном методе, применяется теорема Пифагора к треугольникам, образованным сторонами и диагоналями прямоугольника. Путем подстановки известных значений длин сторон, используя теорему Пифагора, получается выражение, которое подтверждает равенство диагоналей.
| Метод | Описание |
|---|---|
| Символическая алгебра | Применение алгебраических операций и геометрических свойств прямоугольников. |
| Сходство треугольников | Использование свойств сходства треугольников для доказательства равенства диагоналей. |
| Теорема Пифагора | Применение теоремы Пифагора к треугольникам, образованным сторонами и диагоналями прямоугольника. |
Экспериментальные исследования связи между диагоналями прямоугольников
С целью проверки гипотез и получения более полной картины, были проведены серии измерений диагоналей на разнообразных прямоугольниках различных форм и размеров. Полученные результаты анализируются и статистически обрабатываются, чтобы определить возможные закономерности и тренды, существующие в связи между длиной одной диагонали и длиной другой.
В ходе исследований также были учтены факторы, которые могут влиять на соотношение диагоналей, такие как форма и пропорции прямоугольников. Результаты позволяют выяснить, какие факторы сильнее всего влияют на эту связь и какие закономерности наблюдаются при разных условиях эксперимента.
Описанные экспериментальные исследования позволяют все более точно определить природу связи между диагоналями прямоугольников и их основными характеристиками. Результаты данных исследований могут применяться в различных областях, таких как архитектура, инженерия и дизайн, для оптимального использования прямоугольников и прогнозирования их свойств на основе имеющихся параметров.
| Прямоугольник | Длина диагонали 1 | Длина диагонали 2 |
|---|---|---|
| Прямоугольник A | 3.5 | 4.2 |
| Прямоугольник B | 6.1 | 7.5 |
| Прямоугольник C | 5.2 | 5.2 |
Влияние геометрической особенности на различные аспекты прямоугольника
В данном разделе рассмотрим, как равенство диагоналей прямоугольника влияет на другие геометрические характеристики этой фигуры. Знание этой особенности поможет нам лучше понять взаимосвязь между различными свойствами прямоугольника и его структурой.
Взаимосвязь со сторонами: Замечено, что в случае, когда диагонали прямоугольника равны, его стороны также обладают определенными особенностями. Например, пары противоположных сторон являются параллельными и равными между собой, образуя таким образом прямоугольник.
Влияние на углы: Равенство диагоналей прямоугольника имеет важное значение для его углов. Каждый угол равнобедренного прямоугольника (оба основания любого угла равны) составляет половину прямого угла, что обусловлено равенством диагоналей.
Связь с площадью: Равенство диагоналей также оказывает влияние на площадь прямоугольника. Известно, что площадь данной фигуры можно вычислить как произведение длины одной его стороны на длину диагонали. При равенстве диагоналей, площадь прямоугольника упрощается до произведения длин одной стороны на саму себя.
Таким образом, равенство диагоналей прямоугольника является важным фактором, который определяет различные характеристики этой геометрической фигуры. Понимание этого свойства поможет нам лучше анализировать и решать задачи, связанные с прямоугольниками, и использовать их в различных практических ситуациях.
Вопрос-ответ

Что такое свойства прямоугольника?
Свойства прямоугольника – это особенности и характеристики данной геометрической формы, такие как равенство длин сторон, равенство углов, равенство диагоналей и т.д.
Каким образом было доказано равенство диагоналей прямоугольников?
Доказательство равенства диагоналей в прямоугольниках основано на использовании свойств параллельных линий и свойств многоугольников.Основная идея заключается в том, что диагонали прямоугольника делят его на два равных треугольника, и с помощью теоремы о равенстве гипотенуз и катетов в прямоугольных треугольниках можно доказать равенство диагоналей.
Какие еще свойства обладают прямоугольники, кроме равенства диагоналей?
Прямоугольники обладают несколькими свойствами, помимо равенства диагоналей. Например, стороны прямоугольника перпендикулярны друг другу, углы прямоугольника равны по два, длины противоположных сторон равны, а также прямоугольники являются частным случаем параллелограмма.
Какие применения имеет равенство диагоналей в прямоугольниках в реальной жизни?
Равенство диагоналей в прямоугольниках имеет различные применения в реальной жизни. Например, это свойство используется в строительстве для проверки квадратности углов в помещениях или построения равных отрезков. Также равенство диагоналей в прямоугольниках может применяться в геодезии и картографии для вычисления расстояний и определения точных геометрических форм.
Возможны ли исключения для равенства диагоналей в прямоугольниках?
В идеальных условиях и при точном строении прямоугольника, равенство диагоналей является обязательным свойством. Однако в реальности из-за погрешностей измерений и неточности построения возможны незначительные расхождения, которые могут приводить к кажущемуся неравенству диагоналей.
Какое свойство прямоугольников было доказано в данной статье?
В данной статье было доказано свойство равенства диагоналей у прямоугольников.



