Изысканная математика – это не только набор формул и непростых уравнений. В этой науке заключены многие загадки и подзаголовки, составляющие ядро вычислительной мысли. Одной из таких загадок являются понятия "нод" и "нок". Возможно, вы ранее не слышали об этих таинственных аббревиатурах, но они с легкостью могут стать вашими верными спутниками на пути к числовому разнообразию.
Ñод и нок. Звучит как таинственный язык, но на самом деле это сокращения от слов "наибольший общий делитель" и "наименьшее общее кратное". Вдруг между ними скрывается множество численных стратегий и головоломок, готовых раскрыть свои секреты. Представьте, что нод и нок – это пазлы, ожидающие своих игроков и гении, чтобы их разгадать. Они служат проходными билетами в мир цифровых комбинаций и подписаны своими особыми правилами и определениями.
Если первая мысль, которая возникла у вас в голове, – "Я не понимаю математику", то время изменить этот стереотип. Нод и нок доступны и понятны каждому, кто готов раскрыть их суть. Вместе с нами вы изучите простые примеры и шаг за шагом занюхаете ароматы вычислительной науки. Позвольте себе открыть новые горизонты и покорить вершины, о которых вы еще не подозревали. Давайте начнем это захватывающее путешествие в мир чисел и их великих секретов – нод и нок математики!
Значимость нахождения общих делителей и кратных для математики учебной программы в шестом классе

В ходе изучения математики в шестом классе, ученики сталкиваются с концепцией поиска общих делителей и кратных двух или более чисел. Понимание и применение этих понятий имеет важное значение в решении различных задач и проблем, как в математике, так и в повседневной жизни.
Общие делители двух или более чисел - это числа, которые делятся нацело на все эти числа. Например, для чисел 12 и 18 общими делителями будут числа 1, 2, 3 и 6. Понимание общих делителей позволяет ученикам найти наименьший общий делитель (НОД) чисел и использовать его для упрощения дробей или нахождения общего числа предметов.
Кратные числа, с другой стороны, представляют собой числа, которые делятся на заданное число без остатка. Например, для числа 5 все числа 10, 15, 20 и так далее являются кратными числами. Понимание кратных чисел помогает ученикам находить наименьшее общее кратное (НОК) нескольких чисел и использовать его, например, чтобы найти общую периодичность в повторяющихся событиях.
- Поиск наименьшего общего делителя (НОД) двух или более чисел
- Применение НОД при упрощении дробей в математических заданиях
- Нахождение общего числа предметов с помощью НОД
- Поиск наименьшего общего кратного (НОК) нескольких чисел
- Использование НОК для нахождения общей периодичности в повторениях
Расшифровка понятий

В данном разделе мы погрузимся в мир математических терминов, которые используются для определения взаимосвязей и свойств чисел. Разберем основные понятия, которые помогут нам лучше понять и решать математические задачи.
Начнем с термина "наибольший общий делитель" - это числовое понятие, которое указывает на наибольшее число, на которое одновременно делится и первое число, и второе число. Это позволяет нам найти общие делители и определить наибольший из них, что затем может быть использовано для решения различных задач.
Теперь давайте обратим внимание на термин "наименьшее общее кратное". Он относится к наименьшему числу, которое одновременно является кратным и первого числа, и второго числа. Таким образом, мы можем определить кратные числа и найти их наименьшее общее кратное, что поможет нам решить задачи, связанные с периодическими явлениями или повторяющимися событиями.
Понимание этих понятий поможет нам более глубоко исследовать мир чисел и выполнять математические операции с большей точностью и уверенностью
Как определить наибольший общий делитель и наименьшее общее кратное?
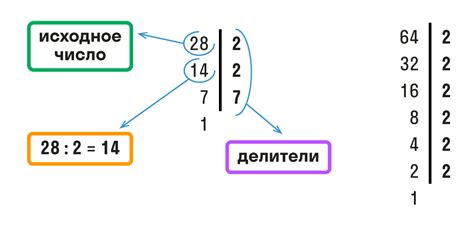
Наибольший общий делитель (НОД) двух или более чисел - это наибольшее число, которое одновременно является делителем каждого из этих чисел. Например, НОД чисел 12 и 18 равен 6, так как 6 делит и 12, и 18 без остатка, а большее число, такое как 9 или 15, не делит оба числа без остатка.
Для вычисления НОД можно использовать различные методы, например: метод деления, алгоритм Евклида или факторизацию чисел на простые множители.
Наименьшее общее кратное (НОК) двух или более чисел - это наименьшее положительное число, которое делится на каждое из этих чисел без остатка. Например, НОК чисел 4 и 6 равен 12, так как 12 делится и на 4, и на 6 без остатка, а меньшее число, такое как 8 или 10, не делится на оба числа без остатка.
Для вычисления НОК также можно использовать различные методы, например: методы вычисления простых множителей или формулу, основанную на НОД.
Примеры использования наибольшего общего делителя и наименьшего общего кратного в решении задач

В математике существуют два важных понятия: наибольший общий делитель (НОД) и наименьшее общее кратное (НОК). Эти понятия играют важную роль в решении разнообразных задач.
- Задача 1: Разделить 72 и 90 на их НОД.
- Решение: Найдем НОД для чисел 72 и 90. Разложим оба числа на простые множители: 72 = 2 × 2 × 2 × 3 × 3, 90 = 2 × 3 × 3 × 5. НОД равен произведению общих простых множителей с наименьшими степенями, поэтому НОД(72, 90) = 2 × 3 × 3 = 18. Деление чисел 72 и 90 на 18 даст ответ: 4 и 5 соответственно.
- Задача 2: Найти наименьшее общее кратное чисел 10 и 15.
- Решение: Для нахождения НОК, мы также разлагаем числа на простые множители: 10 = 2 × 5, 15 = 3 × 5. НОК равно произведению всех простых множителей с наибольшими степенями, поэтому НОК(10, 15) = 2 × 3 × 5 = 30.
- Задача 3: Ответить на вопрос - сколько минут пройдет до ближайшей встречи двух судов, если один судноходец курсирует с интервалом в 40 минут, а второй - с интервалом в 60 минут.
- Решение: Нам нужно найти НОК для чисел 40 и 60. Разложим их на простые множители: 40 = 2 × 2 × 2 × 5, 60 = 2 × 2 × 3 × 5. НОК будет равен произведению всех простых множителей с наибольшими степенями: НОК(40, 60) = 2 × 2 × 2 × 3 × 5 = 120. Таким образом, ближайшая встреча двух судов произойдет через 120 минут.
Примеры использования НОД и НОК в решении задач помогают нам понять, как эти понятия применяются на практике и как они помогают нам решать разнообразные задачи, связанные с числами и интервалами времени.
Вопрос-ответ

Что такое нод и нок в математике?
НОД (наибольший общий делитель) и НОК (наименьшее общее кратное) — это понятия из области арифметики, которые используются для работы с целыми числами. НОД двух чисел - это наибольшее число, на которое оба числа делятся без остатка. НОК двух чисел - это наименьшее число, которое делится на оба числа без остатка.
Как вычислять НОД двух чисел?
Для вычисления НОД двух чисел можно воспользоваться алгоритмом Евклида. Сначала находим остаток от деления большего числа на меньшее, затем повторяем этот процесс для полученных остатков до тех пор, пока не получим остаток равный нулю. На этом этапе полученное ненулевое число и будет НОДом исходных чисел.
Для чего нужны НОД и НОК в математике?
НОД и НОК используются во многих задачах и вычислениях. Например, они могут помочь в сокращении дробей, в решении задач на пропорциональность, нахождении общего знаменателя, планировании повторяющихся событий, а также в других областях математики и ее приложениях.
Какая связь между НОДом и НОКом?
Связь между НОДом и НОКом заключается в следующем: если у нас есть два числа a и b, то их произведение равно произведению НОКа и НОДа этих чисел. Иными словами, НОК(a, b) = (a * b) / НОД(a, b).



