Нет ничего более удивительного, чем узнавать о мире с научной точки зрения. И хотя физические величины и числа могут показаться на первый взгляд связанными понятиями, их сущность и значение отличаются друг от друга как две стороны одной медали.
Существует много различий между физическими величинами и числами, но их главное различие заключается в природе и предназначении. В отличие от чисел, которые представляют абстрактные математические объекты, физические величины являются мерой и описанием реальных явлений и свойств окружающего нас мира. Они помогают нам количественно измерять, анализировать и понимать природу, предоставляя нам уникальную возможность исследования и прогнозирования физических явлений.
Особое значение физических величин заключается в том, что они несут на себе информацию не только о количестве, но и о качестве изучаемых объектов. Это значит, что физическая величина не просто численное значение, а представляет собой объективную характеристику реальности. С помощью физических величин мы можем описывать массу, длину, время, силу и многие другие свойства материи и движения. Каждая физическая величина имеет свою единицу измерения, которая помогает нам стандартизировать измерения и установить общепринятые стандарты.
Таким образом, понимание разницы между физическими величинами и числами позволяет нам глубже познать мир и его законы. Важно помнить, что физические величины обладают уникальными свойствами и значением, отражающими особенности и природу исследуемых явлений. И лишь, осознавая эту грань между математикой и физикой, мы сможем полностью раскрыть прекрасный мир физических законов и явлений, лежащих в основе нашего существования.
Определение физической величины и ее особенности
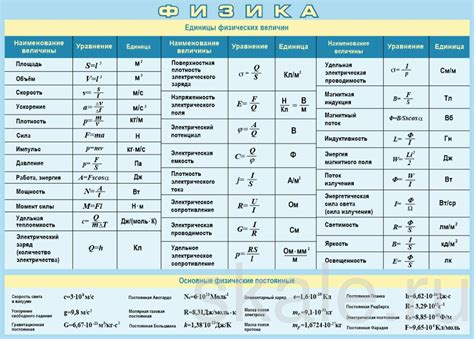
Физические величины обладают несколькими особенностями, которые отличают их от обычных чисел. Во-первых, физические величины имеют размерность, то есть они выражаются в определенных единицах измерения, которые указываются рядом с численным значением. Это позволяет нам понимать, какие единицы измерения используются при описании конкретной физической величины.
Во-вторых, физические величины обладают направленностью или векторной природой, это значит, что они не только имеют определенное численное значение, но и указывают направление их действия или движения. Например, векторные физические величины включают силу, скорость, ускорение и т. д., которые обладают не только численными значениями, но и определенными направлениями.
Наконец, физические величины могут быть связаны между собой различными математическими зависимостями. Они могут быть взаимозависимы или прямо пропорциональны друг другу. Это позволяет нам анализировать физические процессы, предсказывать их результаты и решать различные физические задачи.
Основные отличия числа от физической величины

Когда речь заходит о числе и физической величине, мы сталкиваемся с двумя основными концепциями, которые имеют свои уникальные свойства и значения.
Число – это абстрактный объект, который используется для измерения количества или порядка чего-либо. Оно является результатом абстрактных операций и может представляться различными математическими символами. Число не обладает физическими свойствами, такими как масса, объем или длина. Оно служит лишь для указания количественных характеристик и возможности проведения математических операций.
Физическая величина, напротив, описывает конкретные атрибуты объектов, явлений или процессов в физическом мире. Она имеет измеряемое значение и единицу измерения, которая позволяет сравнивать и оценивать значения величин. Физическая величина может быть связана с размерами, весом, скоростью и другими физическими характеристиками объектов.
| Число | Физическая величина |
|---|---|
| Абстрактный объект | Описывает конкретные атрибуты объектов |
| Используется для измерения количества или порядка | Имеет измеряемое значение |
| Не обладает физическими свойствами | Связана с размерами, весом и другими физическими атрибутами |
Таким образом, числа и физические величины представляют различные аспекты нашего мира. Числа являются абстрактными понятиями, в то время как физические величины отображают конкретные характеристики объектов и процессов. Понимание различий между этими двумя концепциями позволяет нам точно описывать и измерять физическое окружение, а также проводить математические операции на числовых данных.
Роль физических величин в науке и технике

Физические величины характеризуют такие свойства объектов и явлений, как масса, длина, время, температура, скорость и другие. Они являются основой для формулирования законов физики и других научных дисциплин, а также для разработки технических инноваций.
| Примеры физических величин | Значение в науке и технике |
|---|---|
| Масса | Позволяет определить вес объекта, его инерцию и взаимодействие с другими объектами. |
| Сила | Определяет взаимодействие и движение объектов, а также позволяет изучать механические свойства материалов. |
| Энергия | Играет решающую роль в различных физических и химических процессах, а также в производстве и передаче электроэнергии. |
Физические величины не только помогают нам понять природу окружающего нас мира, но и являются основой для разработки новых технологий. Они используются в различных областях, таких как инженерия, медицина, астрономия и многие другие. Благодаря изучению и применению физических величин мы можем создавать более эффективные и инновационные решения, улучшая нашу жизнь и развивая научные и технические отрасли.
Значимость измерения физических величин: реальные аспекты
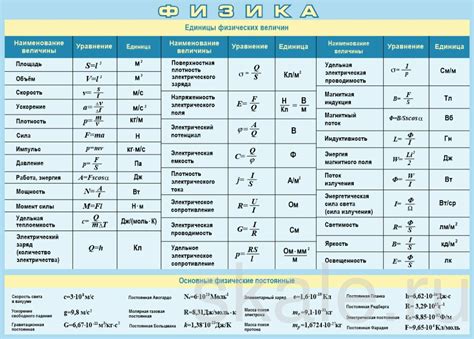
При изучении природных процессов и различных явлений существует необходимость в определении и количественном измерении их свойств. Именно для этой цели применяются физические величины, которые позволяют выразить разнообразные аспекты физической реальности.
Значение измерения физических величин проявляется в практических применениях. Точные и надежные измерения физических величин являются основой для разработки новых технологий, создания инновационных устройств и систем. Инженеры, ученые и другие специалисты различных областей полагаются на значения измерений, чтобы осуществить проектирование, расчеты и принятие решений в своей работе. Все это показывает значимость физических величин и их значений в нашей повседневной жизни.
Кроме того, значения измерения физических величин имеют практическое применение в различных научных исследованиях. Например, в физике значения измерений позволяют подтвердить или опровергнуть гипотезы, проверить идеи и модели, анализировать результаты экспериментов. В медицине значения измерений используются для диагностики различных заболеваний и контроля состояния пациентов. Физические величины и их значения сопутствуют и другим наукам, таким как химия, биология и география, где они являются неотъемлемой частью исследовательского процесса.
В итоге, значение измерения физических величин выходит за рамки простых чисел или абстрактных понятий. Это мощный инструмент, который позволяет нам понять и описать разнообразные аспекты окружающего мира, а также применить полученные знания в нашей повседневной жизни и научных исследованиях.
Математические свойства чисел и физических величин

В данном разделе будет рассмотрено необычайное разнообразие математических свойств чисел и физических величин. Каждая из этих категорий имеет свои особенности и свойства, которые позволяют использовать их в различных областях научного и практического знания.
- Арифметические операции:
- Сравнение и порядок:
- Математические свойства:
- Применение в науке и технике:
Основными арифметическими операциями являются сложение, вычитание, умножение и деление. Числа могут быть складываны, вычитаться, умножаться друг на друга и делиться друг на друга, при этом соблюдая определенные правила и свойства. Аналогично, с физическими величинами можно выполнять арифметические операции, результаты которых отражают законы и принципы физического мира.
Числа могут быть сравниваемы друг с другом с помощью операций "больше", "меньше" и "равно". Таким образом, можно установить порядок чисел на числовой оси. Аналогично, физические величины можно сравнивать и упорядочивать с учетом их значения и единицы измерения.
Числа обладают различными математическими свойствами, такими как ассоциативность, коммутативность, дистрибутивность и другие. Эти свойства позволяют выполнять различные операции с числами и получать точные и последовательные результаты. Физические величины также могут обладать аналогичными математическими свойствами, которые помогают в проведении различных расчетов и анализе данных.
Числа и физические величины являются основными инструментами в научных и технических исследованиях. Они используются для описания и измерения объектов и явлений, а также для формулировки законов и теорий. Математические свойства чисел и физических величин играют ключевую роль в применении этих понятий для решения реальных задач и развития науки и техники.
Физические величины и их системы измерения

Ключевым отличием физических величин от чисел является их фундаментальная связь с конкретными явлениями и объектами в нашем мире. В отличие от абстрактных чисел, физические величины имеют размерность и единицы измерения, которые позволяют нам количественно характеризовать физические процессы. Они могут представлять собой такие разнообразные концепции, как длина, масса, время, скорость, сила, температура и так далее.
Для того чтобы физические величины можно было измерять и сравнивать, важно иметь системы измерения, которые обеспечивают единообразные и взаимно согласованные стандарты измерений. В разных странах и научных областях используются различные системы измерений, такие как СИ (международная система единиц), СГС (сантиметры-граммы-секунды) или англо-американская система.
Использование систем измерений позволяет нам создавать универсальные и согласованные стандарты, которые позволяют сравнивать результаты измерений, обмениваться информацией и строить научные теории и модели, основываясь на объективных данных. Кроме того, системы измерений позволяют проводить эксперименты и оценивать результаты, что является неотъемлемой частью научного метода.
Единицы измерения в физике: международная система VS другие системы
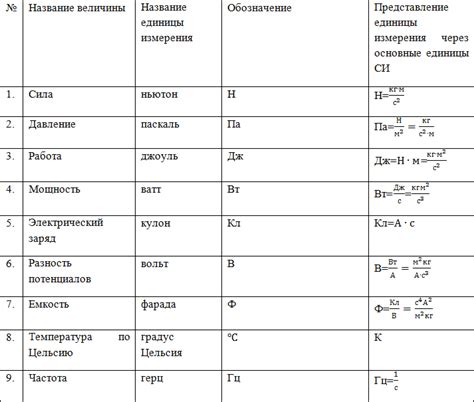
В физике, как и в других естественных науках, измерения играют ключевую роль. Они позволяют нам описывать и анализировать различные физические явления и величины. Однако, чтобы результаты измерений были понятны и сопоставимы между разными исследователями, необходимо использование единиц измерения.
Практическое использование физических величин в повседневной жизни

Перед нами открывается захватывающий мир физических величин, имеющих широкое практическое применение в повседневной жизни. Измерение и использование этих величин помогает нам понять и описать окружающий нас мир, а также решать различные проблемы и задачи.
Одним из самых очевидных примеров практического использования физических величин является измерение времени. Мы постоянно используем время в повседневной жизни, чтобы организовывать свою деятельность, планировать события и принимать решения. Благодаря физической величине времени мы можем быть вовремя на работе, встречаться с друзьями и родными в назначенное время, а также контролировать и управлять процессами, основанными на временных интервалах.
Еще одним примером практического использования физических величин является измерение расстояний. Благодаря физическим величинам, связанным с пространством и движением, мы можем определить и оценить удаленность различных объектов и мест. Измерение расстояний играет важную роль в навигации, путешествиях, строительстве, спорте и многих других областях нашей жизни.
Физические величины также широко используются в науке и технике. В физике, химии, биологии и других научных дисциплинах, мы измеряем и анализируем различные физические параметры, чтобы понять природу явлений и создать новые технологии. Без использования физических величин невозможно было бы разработать множество современных изобретений и достижений, которые в настоящее время облегчают и улучшают нашу жизнь.
| Примеры практического применения физических величин |
|---|
| Измерение скорости движения транспортных средств для контроля безопасности и оптимизации процессов. |
| Использование силы тяжести для определения веса предметов и расчета нагрузки при строительстве. |
| Измерение температуры для контроля климата внутри помещений и разработки новых материалов. |
| Определение давления для контроля работы системы водоснабжения и создания приспособлений для измерения глубины. |
| Измерение электрических величин для разработки электроники, энергосистем и коммуникационных сетей. |
Вопрос-ответ

Чем отличается физическая величина от числа?
Физическая величина представляет собой свойство или характеристику объекта или процесса, которую можно измерить, в то время как число является абстрактным символом, используемым для представления количественной информации.
Каково значение физической величины?
Значение физической величины определяется числовым результатом ее измерения, выраженным в соответствующих единицах измерения. Например, если измерить длину стола с помощью метра, значение физической величины будет числовым результатом этого измерения, выраженным в метрах.
Какие единицы измерения используются для представления физической величины?
Для представления физических величин используются различные системы единиц измерения, такие как Международная система единиц (СИ) и системы CGS (сантиметр-грамм-секунда) или MKS (метр-килограмм-секунда). Например, для измерения длины можно использовать метры или сантиметры в СИ.
В чем особенность измерения физических величин?
Особенностью измерения физических величин является использование приборов и методов, направленных на получение точного и воспроизводимого результата. Измерение должно быть проведено с учетом всех факторов, влияющих на результат, таких как погрешность измерения, инструменты и условия окружающей среды.
Можно ли проводить сравнение и арифметические операции с физическими величинами?
Да, сравнение и арифметические операции между физическими величинами возможны, если они имеют одинаковые размерности. Например, можно сравнивать длину двух объектов или складывать две величины с одинаковой размерностью, такие как сила или время. В этом случае результат будет также иметь ту же размерность.
Что такое физическая величина?
Физическая величина - это свойство или атрибут объекта или явления, которое можно измерить. Она характеризуется числовыми значениями и единицами измерения.



