Понимание логики является одной из ключевых составляющих при изучении информатики. Она олицетворяет мощное орудие, позволяющее анализировать и обрабатывать информацию различной природы с уникальной точностью и эффективностью. Однако, чтобы раскрыть полный потенциал логики, мы должны понять ее научную сущность и практическое применение в нашей современной информационной эпохе.
Логическое мышление особенно полезно в информатике, где мы работаем с бинарными системами и логическими операциями. Она является фундаментальным инструментом для создания и развития алгоритмов, программирования и анализа данных. Через определение и формализацию законов, логика позволяет нам правильно организовывать код и проектировать эффективные алгоритмы, а также просчитывать и предсказывать поведение систем и выявлять ошибки на ранних стадиях.
Эволюция мыслительных процессов в контексте развития информационной науки

Начиная с древних времен, человечество постоянно стремилось систематизировать и логически организовать свои знания и идеи. Развитие логического мышления стало непременным условием для прогресса человечества, от открытия математических закономерностей до создания сложных систем.
С ростом технологий и информационного обмена стало ясно, что необходимо разработать методы для обработки и управления информацией. Именно в этом контексте возникла информатика – наука, изучающая методы обработки информации и ее представление. Логика в информатике играет ключевую роль, позволяя сознательно организовывать все виды информации, а также разрабатывать алгоритмы и решать сложные задачи.
Первые шаги в создании формальных систем для описания логических процессов были сделаны в течение многих веков. Различные философы и ученые внесли свой вклад в развитие логики и создали основные принципы и правила, которые легли в основу современных формальных логических систем. Дальнейшие открытия в математике и логике привели к разработке формальных языков и методов для представления знаний и решения проблем в информатике.
Сегодня логика в информатике имеет широкое применение в различных областях, таких как искусственный интеллект, базы данных, компьютерная архитектура и теория алгоритмов. Формальные логические системы и методы решения проблем играют решающую роль в создании эффективных алгоритмов, разработке баз данных и построении сложных информационных систем.
Аксиомы, также известные как постулаты или базисные истины, представляют собой независимые истинности, которые принимаются без доказательств. Они являются основой для построения логических рассуждений и формулирования теорий. Аксиомы выступают в качестве отправной точки и позволяют сформулировать некоторые основополагающие идеи или утверждения, на которых базируется дальнейшая логическая конструкция.
- Аксиомы являются основой для логического мышления и формулирования теорий.
Роль логики в разработке алгоритмов и программировании
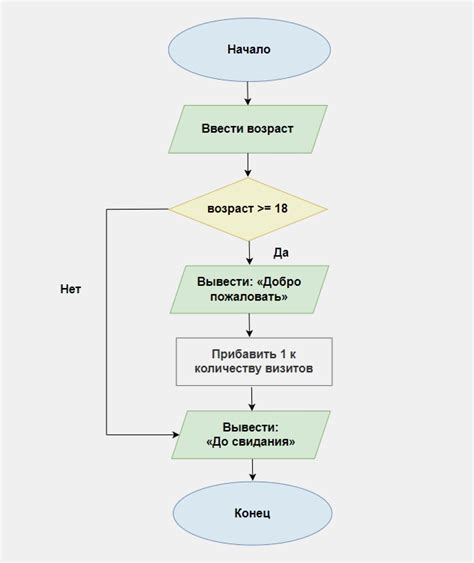
В разработке алгоритмов роль логики заключается в определении последовательности действий, которые должны быть выполнены компьютером для достижения заданной цели. Логические операторы, такие как "если-то" и "иначе", позволяют программистам задавать условия, при которых должны выполняться определенные действия либо выбираться альтернативные варианты.
Логика также активно используется в процессе программирования. При создании программ, важно определить точные спецификации и основные требования к функциональности. Использование логического мышления позволяет программистам анализировать и идентифицировать все возможные варианты развития событий, учитывая различные краевые случаи и условия.
Применение логики в алгоритмах и программировании также способствует повышению эффективности и точности созданных программ. Знание и применение логических принципов позволяет программистам оптимизировать код и обеспечивать более логичную и понятную структуру программы.
Разнообразные подходы к логическому моделированию в компьютерных науках
В информатике есть множество подходов к созданию логических моделей, которые позволяют анализировать и представлять информацию в компьютерных системах. Эти подходы различаются по методам и инструментам, которые используются для описания и решения логических задач.
Также существуют подходы к логическому моделированию, основанные на теории множеств и графах. Эти методы позволяют представлять и анализировать информацию с помощью различных структур, таких как деревья, леса и сети. Использование таких моделей позволяет более эффективно организовывать и обрабатывать данные в информационных системах.
Все эти подходы к логическому моделированию в информатике имеют свои преимущества и ограничения, и выбор конкретного подхода зависит от целей и требований задачи. Важно уметь адаптировать и комбинировать эти подходы для создания гибких и эффективных моделей для анализа и управления информацией.
Различия и ограничения метода логического мышления в информационных технологиях

Изучая вопросы, связанные с применением логического подхода в информатике, мы сталкиваемся с рядом проблем и ограничений, которые заслуживают особого внимания. При анализе и использовании логической системы в информационных технологиях возникают некоторые несовершенства и противоречия, которые связаны с ее ограничениями в определенных контекстах.
Первая проблема, с которой мы сталкиваемся, - это ограничение формализма логического подхода в информатике. И хотя математическая логика обладает определенными преимуществами в обработке информации, она не всегда способна адаптироваться к разнообразным задачам в информационных системах. Это ограничение может привести к недостаточной точности в решении определенных задач, а также к сложностям в представлении нечеткой информации или омрачить возможности достижения оптимальных результатов в некоторых случаях.
Второй аспект, требующий внимания, - это ограничение на возможность логического обобщения в информатике. Во многих случаях применение чисто логического подхода может не позволить получить полное представление о сложных системах или динамичных процессах. Исследователи и применители логического метода в информатике сталкиваются с проблемой объединения и обобщения необходимой информации, что может привести к искажениям или упущению значимых деталей.
Неполное описание контекста является еще одним ограничением логического подхода в информатике. Логика требует четкого формализованного описания правил и условий, но в реальных задачах информационных систем может быть сложно учесть все возможные варианты и исключения, а также учесть контекст, в котором будет применяться логическое рассуждение. Это ограничение представляет определенные проблемы и вызывает сложности при решении задач, связанных с большим объемом и сложностью информации.
Такие ограничения логического подхода в информатике необходимо учитывать при применении данной методологии. Важно помнить, что логическое мышление не всегда является всеобъемлющим и единственно верным методом в информационных технологиях, и его применение должно осуществляться с учетом конкретной задачи и контекста использования.
Логическое программирование и язык Prolog

Программирование по логической парадигме и язык Prolog представляют уникальный подход к разработке программных систем. Они основаны на логической связи между фактами и правилами, которая отражает причинно-следственные отношения в реальном мире.
Логическое программирование похоже на решение логических головоломок, где программа представляет собой набор логических утверждений, а решение проблемы заключается в нахождении комбинаций, удовлетворяющих заданным правилам и фактам.
Язык Prolog является одним из наиболее распространенных и мощных инструментов для логического программирования. Он строится на основе формул логики предикатов и предоставляет возможности для создания и манипулирования логическими отношениями.
Логическое программирование и язык Prolog активно применяются в различных областях, включая искусственный интеллект, экспертные системы, анализ данных, разработку баз знаний и другие. Они позволяют создавать эффективные и гибкие программные решения, основанные на логической модели интерпретации мира.
Точность и строгость рассуждений в компьютерных науках

Точность логического мышления в информатике означает, что каждый шаг в процессе рассуждений должен быть обоснован и логически обоснован. Это важно для достижения правильных результатов и исключения ошибок в вычислениях. Строгое мышление, с другой стороны, подразумевает следование строгим правилам и законам логики, что позволяет проводить логические операции над данными и операционными системами с высокой степенью надежности.
Точность и строгость логического мышления являются основными принципами, лежащими в основе разработки алгоритмов в информатике. Алгоритмы представляют собой набор шагов, описывающих последовательность операций для решения определенной задачи. Четкость и логичность каждого шага алгоритма позволяют точно определить порядок выполнения действий, что является важным фактором для программистов при разработке сложных приложений и систем.
Точность и строгость логического мышления также играют роль в принятии решений в информатике. Важно принимать решения, основанные на логических доводах и объективных фактах, а не на эмоциях или предположениях. Это используется при анализе данных, создании моделей и прогнозировании результатов.
Вопрос-ответ

Что такое научная сущность логики в информатике?
Научная сущность логики в информатике заключается в изучении законов мышления и методов рассуждений, а также разработке формальных систем, которые позволяют корректно описывать и анализировать информацию. Логика является основой для построения алгоритмов и решения сложных задач в информатике.
Какие практические применения имеет логика в информатике?
Логика оказывает значительное влияние на области информатики, такие как искусственный интеллект, теория вычислений, базы данных и программирование. Она помогает разрабатывать и анализировать алгоритмы, оптимизировать работу программ, обеспечивать корректность и надежность систем. Логическое мышление также позволяет эффективно решать проблемы и прогнозировать результаты действий.
Какие законы мышления и методы рассуждений изучает логика в информатике?
Логика изучает класическую и символическую логику, модальную логику, нечеткую логику и другие формальные системы. В рамках этих систем изучаются принципы дедукции, абдукции, индукции, различные виды рассуждений (аналитические, синтетические, интуитивные) и многое другое. Основная задача логики - определить правила, по которым можно строить логические выводы.



