Геометрия - это одна из древних наук, изучающих форму и пространственное строение объектов. Одной из ключевых тем геометрии является изучение многогранников, которые являются фундаментальными элементами в этой науке.
Многогранники олицетворяют собой объекты с ограниченной поверхностью и определенным количеством граней, ребер и вершин. Их наличие делает многогранники особенно интересными для геометров, поскольку эти объекты отражают принципы и законы пространственного строения.
Когда мы говорим о гранях многогранников, мы имеем в виду плоские многоугольники, составляющие поверхность объекта. Ребра между гранями являются ребрами многогранника и представляют собой отрезки, соединяющие вершины. Вершины, в свою очередь, являются точками пересечения ребер.
Понятие граней, ребер и вершин многогранников имеет фундаментальное значение в геометрии и находит свое применение в различных областях нашей жизни. Поэтому понимание этих элементов является ключевым моментом в изучении геометрии и рассмотрении различных пространственных структур.
Зачем нужны многогранники?

Основные характеристики многогранников: взгляд в глубину многоугольных тел

Многогранники представляют собой уникальные фигуры, которые характеризуются не только своими гранями, ребрами и вершинами, но и другими важными характеристиками. Разберемся подробнее в основных особенностях этих трехмерных объектов и их свойствах.
| Характеристика | Описание |
|---|---|
| Число граней | Количество плоских полигонов, ограниченных ребрами. Грани отображают внешнюю оболочку многогранника. |
| Число ребер | Количество ребер, соединяющих вершины. Ребра задают структурную целостность многогранника. |
| Число вершин | Количество точек, в которых пересекаются ребра. Вершины являются угловыми точками многогранника и определяют его форму. |
| Вид многогранника | В зависимости от числа граней, ребер и вершин, многогранники могут быть классифицированы различными способами: они могут быть правильными, неправильными, выпуклыми или невыпуклыми. |
| Размерность | Многогранники могут быть трехмерными (3D) или иметь более высокую размерность. Размерность определяется количеством осей, вдоль которых могут перемещаться точки многогранника. |
Понимание этих основных характеристик позволяет получить более глубокое представление о многогранниках и их разнообразии. Погружаясь в мир граней, ребер и вершин, мы открываем новые возможности для изучения и применения этих уникальных геометрических образований.
Примеры использования геометрических фигур в практике
В современном мире многогранники, такие как призмы, пирамиды, кубы и додекаэдры, находят широкое применение в различных сферах деятельности. Их геометрические свойства и структуры могут быть использованы для решения разнообразных задач и создания функциональных объектов.
Например, в архитектуре многогранники служат основой для проектирования и строительства зданий и сооружений. Грани многогранников определяют форму и структуру здания, а вершины и ребра позволяют определить его пространственные характеристики. От знания свойств многогранников зависит как эстетическая привлекательность, так и функциональность архитектурного объекта.
В инженерии многогранники применяются для создания деталей и механизмов. Например, геометрические фигуры могут использоваться для создания инновационных авиационных двигателей, оптимизации формы крыла самолета или разработки сложных систем промышленной автоматизации. Высокая точность и простота моделирования многогранников делает их ценным инструментом для инженерных расчетов и проектирования.
Многогранники также находят применение в медицине и биологии. В моделировании пространства молекул и белков многогранники позволяют уточнять структуру атомов и предсказывать их свойства. Это позволяет исследователям разрабатывать новые лекарственные препараты и технологии, а также понять механизмы развития различных заболеваний.
Кроме того, многогранники активно используются в графике и дизайне. Их геометрическая структура и форма позволяют создавать эффектные и красочные композиции, а также определять пропорции объектов на иллюстрациях, визуализациях и рекламных материалах. Моделирование и визуализация многогранников становятся неотъемлемой частью работы дизайнера и арт-директора.
Особенности граней многогранника: основные характеристики и их значение
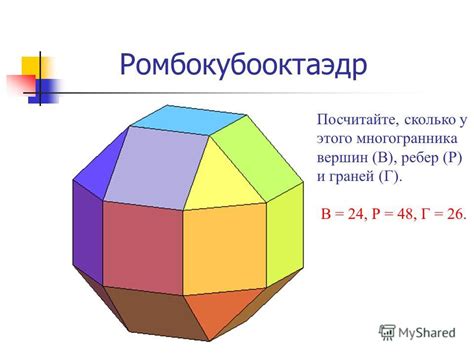
Грани многогранника - это плоские многоугольные поверхности, ограниченные ребрами и составляющие его внешнюю оболочку. Грани являются визуально заметными и обладают своими особенностями и характеристиками, определяющими форму и структуру многогранника.
Каждая грань может быть характеризована несколькими важными параметрами, включая:
- Количество вершин - число точек пересечения грани с ребрами многогранника. От количества вершин зависит форма грани - она может быть треугольной, четырехугольной, пятиугольной и так далее.
- Форма и размеры - каждая грань может быть выпуклой или невыпуклой, а ее размеры могут иметь различные значения, определяющие площадь и периметр грани.
- Ориентация - грань может быть ориентирована в пространстве определенным образом, что влияет на взаимное расположение граней и форму многогранника в целом.
Разнообразие видов граней в многогранниках

В многогранниках, простых геометрических фигурах, которые состоят из набора плоских граней, обнаруживается высокая степень разнообразия этих граней. В зависимости от формы и особенностей геометрической структуры многогранника, грани могут варьироваться в своем количестве, ориентации и взаимном расположении.
Каждая грань в многограннике представляет собой плоскую поверхность, ограниченную ребрами и вершинами. Грани могут быть как прямоугольными и треугольными, так и сборными из различных геометрических форм. Они могут быть выпуклыми, конкавными или иметь сложную форму с выступами и углублениями.
Кроме формы, грани также различаются по углам, которые они образуют с другими гранями и плоскостями многогранника. Эти углы могут быть острыми, прямыми или тупыми, что отражает особенности взаимного взаимодействия граней внутри многогранника.
Некоторые грани в многограннике могут быть параллельными друг другу, в то время как другие пересекаются под различными углами. Это создает интересные геометрические эффекты и позволяет нам исследовать различные комбинации форм, объединенных в одном многограннике.
Изучение разнообразия видов граней в многогранниках позволяет лучше понять их структуру и характеристики. Это знание является важным в геометрии и применяется в различных областях, включая архитектуру, графику и топологию.
Свойства и особенности поверхностей многогранников
Каждая грань многогранника обладает рядом уникальных свойств, которые варьируются в зависимости от их типа и расположения. Одним из ключевых свойств грани является ее площадь, которая определяет степень участия данной поверхности в формировании общей площади многогранника. Также, грани обладают высотой, которая представляет собой расстояние от плоскости грани до наиболее удаленной точки этой грани.
| Тип грани | Описание особенностей |
|---|---|
| Плоская грань | Обладает однородной площадью и нулевой высотой. Является основным типом грани и образует границу между смежными гранями. |
| Угловая грань | Образуется при пересечении двух или более плоских граней многогранника. Имеет нулевую площадь и ненулевую высоту. |
| Косая грань | Характеризуется неравномерной площадью и высотой. Образуется при пересечении граней под непрямым углом. |
| Сферическая грань | Имеет форму сферы и образуется при неравномерном сжатии или растяжении многогранника. |
Комбинация различных типов граней в многограннике создает его уникальную структуру и форму. Изучение свойств и особенностей граней позволяет более глубоко понять и визуализировать взаимоотношение между элементами многогранников и их влияние на общую форму. Также, эти свойства используются при классификации и систематизации многогранников.
Ребра многогранника: структура и свойства
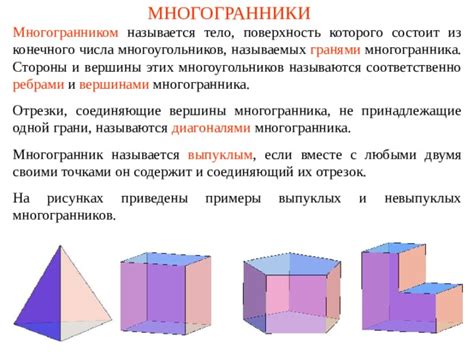
Каждое ребро обладает рядом характеристик, таких как длина, направление и положение в пространстве. Длина ребра является одной из ключевых характеристик, так как она определяет его масштаб и пропорции внутри многогранника. Ребра также имеют направление, которое указывает на ту сторону, вдоль которой они простираются.
Важной особенностью ребер является их положение в пространстве. Они могут быть расположены на поверхности многогранника (внутренние ребра) или выступать из его границ (внешние ребра). Внутренние ребра соединяют вершины внутри многогранника, обеспечивая его компактность и стабильность. Внешние ребра позволяют нам визуализировать форму и структуру многогранника.
Все ребра многогранника взаимно пересекаются или касаются и не могут быть параллелельными друг другу. Их положение и поведение сильно зависят от граней и вершин, с которыми они соединены. Ребра многогранника образуют его скелет и являются основными элементами, которые дают ему прочность и устойчивость в пространстве.
С помощью таблицы можно легко представить свойства и характеристики ребер многогранника:
| Свойство ребер | Описание |
|---|---|
| Длина | Расстояние между вершинами, определяющими ребро |
| Направление | Указывает на сторону, вдоль которой простирается ребро |
| Положение | Внутри многогранника (внутренние ребра) или из границы многогранника (внешние ребра) |
Таким образом, ребра многогранника не только определяют его форму, но и обладают рядом характеристик и свойств, которые влияют на его структуру и прочность. Изучение ребер позволяет более глубоко понять многогранники и их особенности в трехмерном пространстве.
Структура краев многогранников и их связь со гранями
При изучении многогранников особую роль играют их края, которые имеют свою специфическую структуру и тесно связаны с гранями. Края многогранников представляют собой линейные сегменты, которые образуют границы различных граней многогранника.
Края подобно столбикам украшают и определяют форму многогранника, соединяя вершины и образуя разнообразные углы и пересечения между собой. Имеется несколько типов краев многогранников, включая ребра, ребра-диагонали и ребра-рёбра. Каждый тип края имеет свои уникальные свойства и структуру.
- Ребра представляют собой отрезки, соединяющие две соседние вершины многогранника. Они являются основными элементами структуры многогранника и определяют его форму.
- Ребра-диагонали соединяют вершины, не являющиеся соседними, и позволяют создавать внутренние сегменты внутри граней многогранника. Они добавляют дополнительные межгранные связи и увеличивают количество возможных комбинаций граней.
- Ребра-рёбра соединяют соседние рёбра и являются элементами скелета многогранника. Они формируют основу для создания сложных форм и обеспечивают дополнительные опорные точки для построения дополнительных граней.
Изучение структуры краев многогранников позволяет лучше понять их геометрическое устройство и взаимосвязь с гранями. Края определяют форму, жесткость и гибкость многогранника, а также обеспечивают основу для анализа его эйлеровой характеристики и других характеристик. Знание о структуре краев многогранников является важным элементом при решении различных задач в геометрии и теории многогранников.
Вопрос-ответ

Что такое многогранник?
Многогранник - это фигура в трехмерном пространстве, ограниченная плоскими многоугольниками, называемыми гранями. Он также имеет ребра - отрезки, соединяющие вершины граней, и вершины - точки, где пересекаются ребра.
Чем грань многогранника отличается от ребра?
Грань многогранника - это плоский многоугольник, который ограничивает пространство многогранника. Ребро же - это отрезок, который соединяет две вершины граней и определяет их взаимное положение.
Сколько вершин может быть у многогранника?
Количество вершин в многограннике может быть разным в зависимости от его формы. Например, у пирамиды может быть одна вершина, у куба - восемь вершин, а у додекаэдра - двенадцать вершин.
Как определить количество ребер у многогранника?
Количество ребер в многограннике зависит от его формы и количества граней. Оно может быть рассчитано по формуле Эйлера: v - e + f = 2, где v - количество вершин, e - количество ребер, f - количество граней.
Можете привести примеры реальных объектов, которые являются многогранниками?
Конечно! Некоторые примеры многогранников в реальной жизни включают куб, тетраэдр (пирамиду), октаэдр, икосаэдр и додекаэдр. Также кристаллы, такие как алмаз и рубин, также можно рассматривать как многогранники.
Что такое многогранник?
Многогранник - это геометрическое тело, ограниченное плоскими фигурами, называемыми гранями. У многогранника также есть ребра - отрезки линий, соединяющие вершины многогранника. Вершины многогранника являются точками пересечения ребер.



