В современном информационном обществе, где цифровые технологии проникают во все сферы нашей жизни, вопрос безопасности данных становится все более злободневным. Один из ключевых моментов в обеспечении конфиденциальности и неприступности информации – это ее шифрование. Шифрование позволяет защитить данные от несанкционированного доступа и прослушивания, обеспечивая тем самым безопасность личных данных, коммерческой информации и государственных секретов.
Одним из наиболее распространенных алгоритмов шифрования является RSA. RSA – это криптографический алгоритм, разработанный в 1977 году ведущими учеными Ривестом, Шамиром и Адлеманом. Отличительной особенностью алгоритма RSA является использование двух разных ключей: открытого и закрытого. При этом, зашифровать информацию с помощью открытого ключа может каждый пользователь, но расшифровать его сможет только владелец соответствующего закрытого ключа.
Принцип работы алгоритма RSA основан на сложности факторизации больших простых чисел. Это означает, что невозможно найти закрытый ключ, зная только открытый ключ – для этого необходимо произвести разложение на множители большого числа. При этом, алгоритм RSA обладает высокой степенью надежности и стойкости к взлому с использованием современных компьютерных технологий.
Таким образом, алгоритм RSA является одним из основных инструментов в области шифрования данных и обеспечения их безопасности в цифровой среде. За счет использования двух разных ключей и сложности факторизации больших простых чисел, RSA обеспечивает высокую степень защиты от несанкционированного доступа, делая его незаменимым в сфере информационной безопасности.
Основы функционирования криптографической схемы RSA

Для полного понимания принципов работы сложной и надежной системы шифрования RSA необходимо, прежде всего, ознакомиться с ее базовыми компонентами и некоторыми ключевыми понятиями. Алгоритм активно использует математические операции и принципы, чтобы защитить информацию от несанкционированного доступа и обеспечить ее конфиденциальность и целостность.
Центральной идеей RSA является использование двух различных простых чисел, которые фигурируют как основа для формирования пары целочисленных значений. Одно из этих чисел становится публичным ключом, доступным для всех, а другое остается в тайне и служит приватным ключом. Сочетание этих ключей обеспечивает систему шифрования, которую невозможно безопасно взломать без знания приватного ключа.
Важным принципом работы алгоритма RSA является его способность создавать шифры, которые стойко защищают информацию даже при наличии огромного количества вычислительных мощностей и времени. Благодаря использованию математических функций, сложного преобразования данных и уникальных свойств простых чисел, шифрование RSA гарантирует высокий уровень безопасности при передаче конфиденциальной информации.
Криптографические основы

Этот раздел посвящен криптографическим основам, на которых строится алгоритм RSA. Мы рассмотрим принципы, на которых основывается этот алгоритм, включая генерацию ключей и обеспечение безопасности передаваемых данных.
Криптография – это наука о методах защиты информации от несанкционированного доступа. Основной задачей криптографии является обеспечение конфиденциальности и целостности передаваемых данных. В этом разделе мы рассмотрим основные принципы, которые позволяют достичь этих целей.
Ключевой элемент криптографии является использование ключей. Ключи - это особые последовательности символов или чисел, которые используются для преобразования информации. Алгоритм RSA использует пару ключей: открытый и закрытый. Каждый ключ выполняет определенные функции, гарантируя безопасность и аутентификацию данных.
Одной из основных особенностей алгоритма RSA является его математическая сложность, которая обеспечивает высокий уровень безопасности передаваемых данных. RSA основан на задаче факторизации больших чисел, которая является вычислительно сложной. Благодаря этому алгоритму RSA широко применяется для защиты информации в различных областях, включая электронную коммерцию и интернет-коммуникации.
Математические операции и защита информации
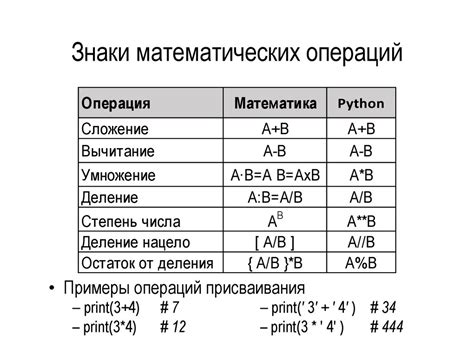
В данном разделе рассматриваются основные математические операции, которые лежат в основе шифрования данных, и их взаимосвязь с обеспечением безопасности информации.
Шифрование данных основано на математических принципах, которые помогают обеспечить конфиденциальность передаваемых сообщений и защитить их от несанкционированного доступа. В этом разделе мы рассмотрим основные операции, такие как возведение в степень и нахождение остатка от деления, которые применяются при создании и использовании шифров алгоритма RSA.
Возведение в степень является ключевой операцией RSA, которая позволяет шифровать и расшифровывать данные. За счет использования больших целых чисел и сложности обратного преобразования, уникальные ключи могут быть сгенерированы и использованы для защиты информации.
Одним из основных преимуществ алгоритма RSA является его сложность взлома, которая связана с трудоемкостью факторизации больших целых чисел. В результате, угадать или вычислить секретные ключи становится практически невозможно для злоумышленников.
| Операция | Описание |
|---|---|
| Возведение в степень | Операция, позволяющая получить результат, который является произведением числа на само себя несколько раз. |
| Нахождение остатка от деления | Операция, результатом которой является остаток от деления одного числа на другое. |
Использование этих математических операций в алгоритме RSA обеспечивает надежность и безопасность передаваемых данных. В дополнение к этому, алгоритм также использует другие уникальные математические принципы, которые помогают сделать его эффективным и надежным инструментом для шифрования информации.
Генерация и применение шифровальных пар в алгоритме RSA

Первый этап - генерация двух простых чисел, которые будут использоваться для создания ключей. Эти числа должны быть большими и достаточно случайными, чтобы предотвратить возможность их факторизации или предсказания. Затем производится математическая операция, известная как "произведение" этих двух чисел, что дает нам модуль, который будет использоваться в дальнейших вычислениях.
Второй этап - выбор открытого ключа, который будет использоваться для шифрования данных. Открытый ключ состоит из двух частей: показателя шифрования и модуля. Показатель шифрования выбирается таким образом, чтобы он был взаимно простым с функцией Эйлера от модуля. Это обеспечивает высокую степень безопасности стандарта RSA.
Третий этап - вычисление закрытого ключа, который будет использоваться для расшифровки данных. Закрытый ключ состоит из двух частей: показателя расшифровки и модуля. Показатель расшифровки вычисляется с использованием расширенного алгоритма Евклида и позволяет получить численное значение, обратное открытому ключу.
Когда ключи созданы, они могут быть использованы для шифрования и расшифровки данных. Открытый ключ используется для зашифровки сообщений перед отправкой, а закрытый ключ - для расшифровки полученных данных. При правильной генерации и использовании ключей, алгоритм RSA обеспечивает высокую степень безопасности и защищает данные от несанкционированного доступа.
Процесс генерации ключей

В этом разделе мы рассмотрим важный этап работы с криптографическим алгоритмом, который позволяет обеспечить безопасность передаваемой информации. Речь пойдет о процессе генерации ключей, которые играют решающую роль в шифровании и расшифровании данных.
При создании шифрованного сообщения необходимо иметь два разных ключа: открытый и закрытый. В процессе генерации ключей используется сложный математический алгоритм, который обеспечивает их достаточную длину и уникальность.
Генерация ключей начинается с выбора двух простых чисел, которые являются основой для создания шифрованной пары. Затем происходит выполнение ряда операций с этими числами, которые включают в себя операции возведения в степень, вычисления остатка при делении и нахождения наибольшего общего делителя.
В результате этих математических манипуляций возникает открытый и закрытый ключи. Открытый ключ предназначен для зашифрования данных и может быть свободно распространен, в то время как закрытый ключ должен быть строго охраняем и использован только для расшифровки.
Генерация ключей в алгоритме RSA обеспечивает высокую степень безопасности передаваемой информации, так как основана на сложности факторизации больших простых чисел. Это делает алгоритм практически неразрешимым для взлома без знания закрытого ключа, что обеспечивает конфиденциальность и целостность данных.
Вопрос-ответ

Как работает алгоритм RSA?
Алгоритм RSA использует принципы криптографии с открытым ключом. Он основан на сложности факторизации больших чисел. В начале процесса генерируются два простых числа, которые являются частью закрытого ключа. Затем вычисляются числа, связанные с этими простыми числами, и формируются открытый ключ и закрытый ключ. Открытый ключ используется для шифрования сообщений, а закрытый ключ - для расшифровки. При шифровании данных, открытый ключ умножается на сообщение, а затем полученное значение возводится в степень открытого ключа по модулю. Для расшифровки используется закрытый ключ, который позволяет возвести зашифрованные данные в степень закрытого ключа по модулю. Это позволяет получить исходное сообщение.
Какие ключи используются в алгоритме RSA?
Алгоритм RSA использует два ключа: открытый ключ и закрытый ключ. Открытый ключ предназначен для шифрования данных и обычно распространяется публично. Он состоит из двух чисел: модуля и показателя степени. Модуль - это результат перемножения двух простых чисел, которые являются частью закрытого ключа. Показатель степени - это число, которое определяет, в какую степень нужно возвести шифруемые данные. Закрытый ключ является секретным и используется для расшифровки данных. Он также состоит из двух чисел: модуля и другого показателя степени, который является обратным к показателю степени открытого ключа по модулю.
На сколько безопасен алгоритм RSA?
Алгоритм RSA считается одним из самых безопасных алгоритмов шифрования, но его безопасность зависит от длины ключа. Чем длиннее ключ, тем сложнее его взломать. Для большинства применений рекомендуется использовать ключи длиной не менее 2048 бит. Однако, с развитием компьютерных технологий и квантовых компьютеров, которые могут в будущем стать способными взламывать RSA, требуется использование ключей ещё большей длины или использование альтернативных алгоритмов шифрования.



